If a chord is drawn through the point of a tangent to circle, then the angles which this chord makes with the given tangent are respectively equal to the angles formed in the corresponding alternate segment.
In the fig., PQ is a tangent to the circle at P. QRS is a straight line. Find the value of x. 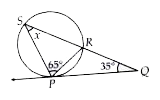
The correct Answer is:D
Topper's Solved these Questions
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Comprehension (Passage-Ii))
4 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Comprehension (Passage-III))
4 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Assertion & Reason)
6 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
- CO-ORDINATE GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Olympiad/HOTS Corner
40 Videos
Similar Questions
If a chord is drawn through the point of contact of a tangent to a circle; then the angle which this chord makes with the given tangent are equal respectively to the angles formed in the corresponding alternate segments.
View SolutionIn the given is the centre of circle, PQ is a tangent to the circle at A. If ∠BAQ=60∘ then find ∠ABCand∠APB.

View Solution
Knowledge Check
If a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
A30∘B60∘C90∘D120∘From an external point two tangents to a circle are drawn. The chord passing through the points of contact subtends an angle 72∘ at the centre. The angle between the tangents is
A36∘B72∘C108∘D144∘
Prove that the tangents at the extremities of any chord make equal angles with the chord.
View SolutionProve that the tangents at the extremities of any chord make equal angles with the chord.
View SolutionIf a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
View SolutionIn Fig RQ is a chord of the circle and POQ is its diameter such that ∠RPQ=30∘. If QT is the tangent to the circle at the point Q them find ∠RQT.
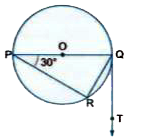
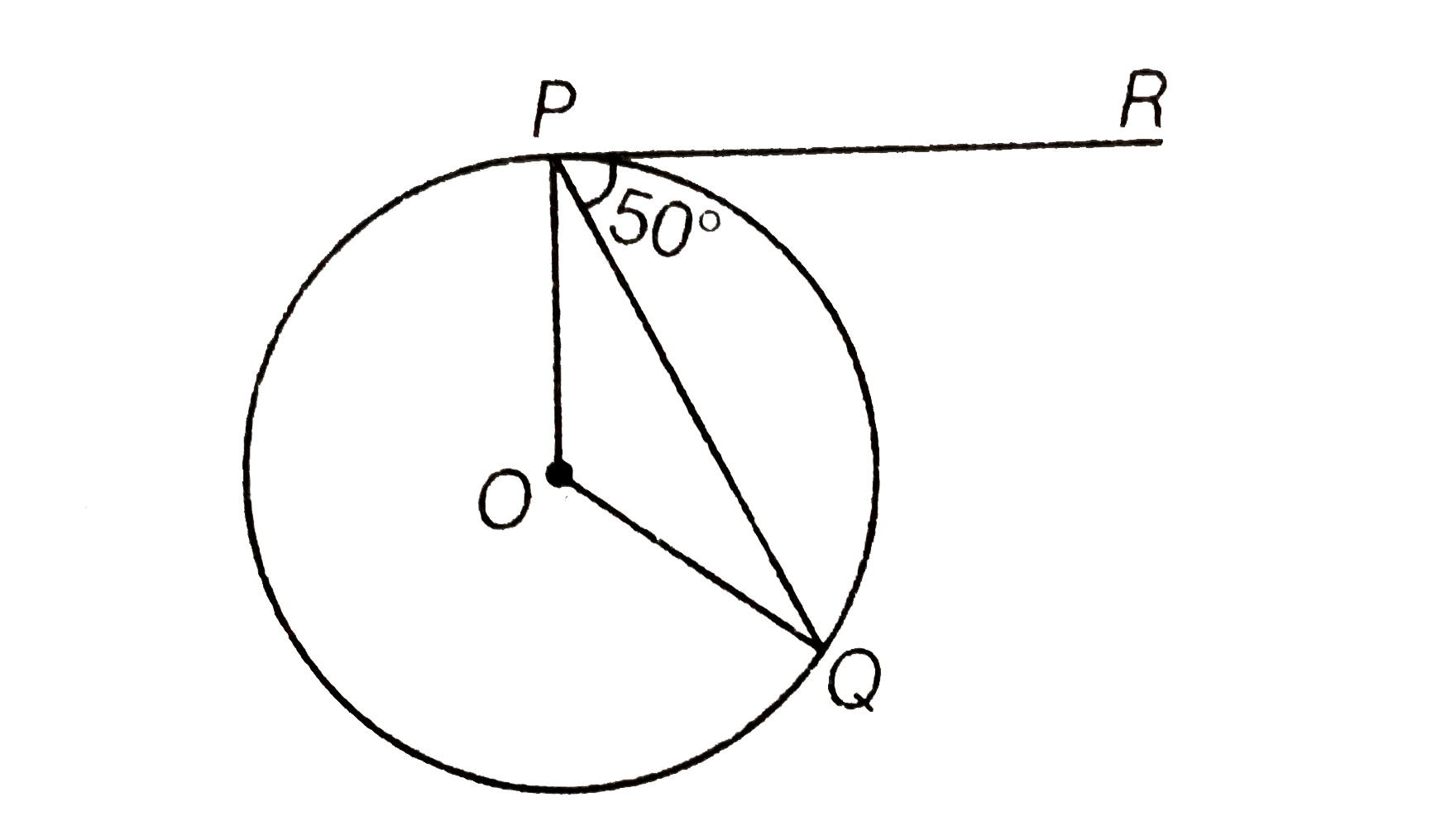
View SolutionIn figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ, then ∠POQ is equal to
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View Solution
