Electric field strength E , max charge = q. Find K = ?
To solve the problem of finding the dielectric constant K given the electric field strength E and maximum charge q, we can follow these steps:
1. Understanding the relationship between charge, capacitance, and potential:
The potential V across a capacitor is given by the formula:
V=qC
where q is the charge and C is the capacitance.
2. Expressing capacitance with dielectric constant:
The capacitance C of a parallel plate capacitor with a dielectric material is given by:
C=K⋅ϵ0⋅Ad
where K is the dielectric constant, ϵ0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
3. Relating electric field E to potential V:
The electric field E between the plates of a capacitor is related to the potential V and the distance d by:
E=Vd
4. Substituting potential V in terms of charge q:
From the previous equations, we can substitute V in the equation for E:
E=qC⋅d
5. Substituting the expression for capacitance C:
Now, substituting C from step 2 into the equation for E:
E=qK⋅ϵ0⋅Ad⋅d
Simplifying this gives:
E=qK⋅ϵ0⋅A
6. Rearranging to find K:
To isolate K, we can rearrange the equation:
K=qE⋅ϵ0⋅A
Final Result:
Thus, the dielectric constant K is given by:
K=qE⋅ϵ0⋅A
The potential V across a capacitor is given by the formula:
V=qC
where q is the charge and C is the capacitance.
The capacitance C of a parallel plate capacitor with a dielectric material is given by:
C=K⋅ϵ0⋅Ad
where K is the dielectric constant, ϵ0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
The electric field E between the plates of a capacitor is related to the potential V and the distance d by:
E=Vd
From the previous equations, we can substitute V in the equation for E:
E=qC⋅d
Now, substituting C from step 2 into the equation for E:
E=qK⋅ϵ0⋅Ad⋅d
Simplifying this gives:
E=qK⋅ϵ0⋅A
To isolate K, we can rearrange the equation:
K=qE⋅ϵ0⋅A
Thus, the dielectric constant K is given by:
K=qE⋅ϵ0⋅A
Topper's Solved these Questions
Similar Questions
In an uniform electric field of strength E, a charge particle Q moves point A to point B in the direction of the field and back from B to A. Calculate the ratio of the work done by the electric field in taking the charge particle from A to B and from B to A.
View SolutionThe electric field strength at a distance r from a charge q is E. What will be electric field strength if the distance of the observation point is increased to 2r (A) E2 (B) E4 (C) E6 (D) none of the above
View Solution
Knowledge Check
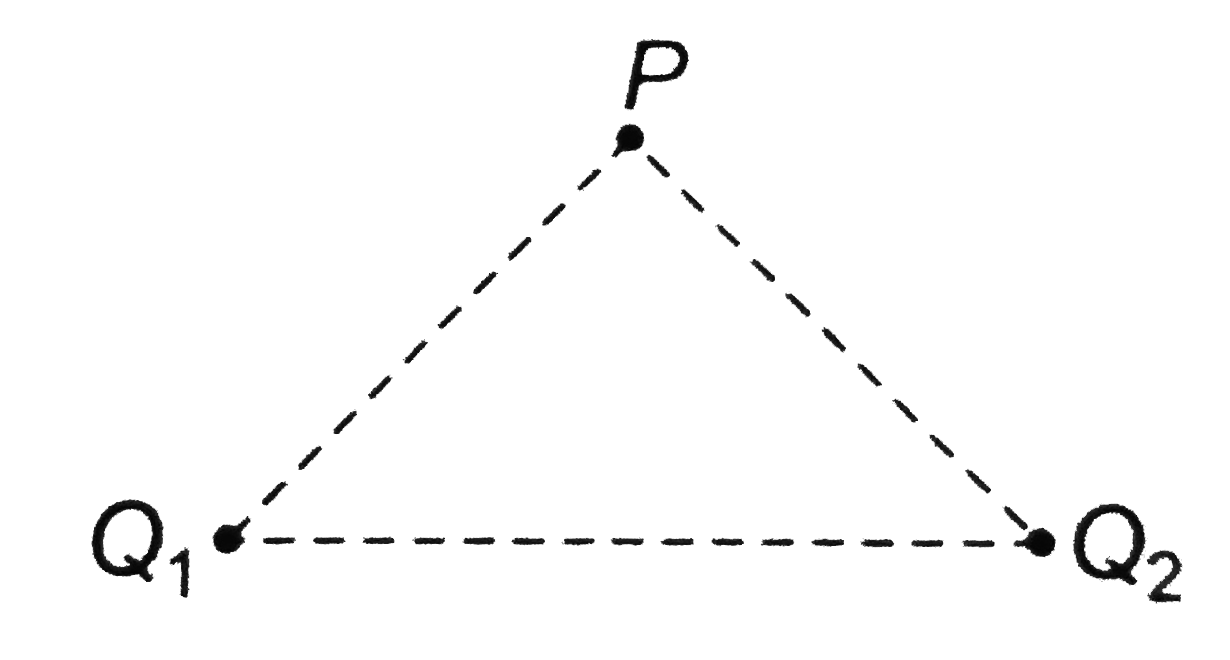
Figure shown a charged conductor resting on an insulating stand. If at the point P the charge density is σ, the potential is V and the electric field strength is E, what are the values of these quantities at point Q ?
 ACharge densityPotentialElectric intensity>σ>V>EBCharge densityPotentialElectric intensity>σV>ECCharge densityPotentialElectric intensity<σVEDCharge densityPotentialElectric intensity<σV<E
ACharge densityPotentialElectric intensity>σ>V>EBCharge densityPotentialElectric intensity>σV>ECCharge densityPotentialElectric intensity<σVEDCharge densityPotentialElectric intensity<σV<EIn figure below, the point charge Q1 causes an electric potential of 60V and an electric field strength of 30Vm−1 at P. and the point charge Q2 separately causes a potential of 120V and a field strength of 40Vm−1 at P.
Which one the following gives possible value of potential and field strength at P due to joint action of Q1 and Q2 ?
 APotential/V, Field/Vm−1
APotential/V, Field/Vm−1
180, 70BPotential/V, Field/Vm−1
180, 50CPotential /V, Field /Vm−1
135, 50DPotential /V, Field /Vm−1
60, 10A protons of mass m charge c is released form rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is
A√2demEB√2dmEeC√2dEmeD√2dEedm
find the electric field strength due to a point charge of 5μC at a distance of 80 cm from the charge.
View SolutionFind the electric field strength due to 5μC of charge at point 30 m away from it in air.
View SolutionA protons of mass m charge 2 e is released from rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is..
View SolutionA point charge q moves unifromly and rectilnearly with a relativistic with a relativistic velocity of light (β=v/c). Find the electric field strength E produced by the charge at the point whose radius vector relatives to the charge is equal to r and forms an angle θ with its velocity vector.
View SolutionThere is a uniform horizontal electric field of strength E in a region. A pendulum bob is pulled to make the string horizontal and released. The bob has mass m and charge q. (a) Find the maximum angle (θ0) that the bob swings before coming to rest momentarily. (b) Find E if the bob comes to rest when the string is vertical.
View Solution
