If at the centre of circular current carrying coil, magnetic field is B0 then the magnetic field at distance r/2 from on the axis of a coil from centre is
To find the magnetic field at a distance r2 from the center of a circular current-carrying coil, we can follow these steps:
Step 1: Understand the Magnetic Field at the Center of the Coil
The magnetic field B0 at the center of a circular current-carrying coil is given by the formula:
B0=μ0I2r
where:
- μ0 is the permeability of free space,
- I is the current flowing through the coil,
- r is the radius of the coil.
Step 2: Identify the Point of Interest
We need to find the magnetic field at a point P located at a distance r2 along the axis of the coil from its center.
Step 3: Use the Formula for Magnetic Field on the Axis of a Circular Coil
The magnetic field BP at a distance x from the center along the axis of the coil can be expressed as:
BP=μ0Ir22(r2+x2)3/2
In our case, x=r2.
Step 4: Substitute x into the Formula
Substituting x=r2 into the formula:
BP=μ0Ir22(r2+(r2)2)3/2
Calculating r2+(r2)2:
r2+r24=4r24+r24=5r24
Thus, we have:
BP=μ0Ir22(5r24)3/2
Step 5: Simplify the Expression
Calculating (5r24)3/2:
(5r24)3/2=(53/2)(r3)(43/2)=5√5r38
Substituting this back into the expression for BP:
BP=μ0Ir22⋅5√5r38=8μ0Ir210√5r3=4μ0I5√5r
Step 6: Relate BP to B0
Now, we can express BP in terms of B0:
BP=45√5B0
since B0=μ0I2r.
Final Result
Thus, the magnetic field at a distance r2 from the center of the coil is:
BP=45√5B0
The magnetic field B0 at the center of a circular current-carrying coil is given by the formula:
B0=μ0I2r
where:
- μ0 is the permeability of free space,
- I is the current flowing through the coil,
- r is the radius of the coil.
We need to find the magnetic field at a point P located at a distance r2 along the axis of the coil from its center.
The magnetic field BP at a distance x from the center along the axis of the coil can be expressed as:
BP=μ0Ir22(r2+x2)3/2
In our case, x=r2.
Substituting x=r2 into the formula:
BP=μ0Ir22(r2+(r2)2)3/2
Calculating r2+(r2)2:
r2+r24=4r24+r24=5r24
Thus, we have:
BP=μ0Ir22(5r24)3/2
Calculating (5r24)3/2:
(5r24)3/2=(53/2)(r3)(43/2)=5√5r38
Substituting this back into the expression for BP:
BP=μ0Ir22⋅5√5r38=8μ0Ir210√5r3=4μ0I5√5r
Now, we can express BP in terms of B0:
BP=45√5B0
since B0=μ0I2r.
Thus, the magnetic field at a distance r2 from the center of the coil is:
BP=45√5B0
Topper's Solved these Questions
Similar Questions
(a) A circular current carrying coil has a radius R. Find magnetic field (a) at centre and (b) along the axis of coil distant √3R from centre. The coil is having N turns and carriers a current i.
(b) Two concentric coil A and B, having current i and 2i and radii 2R and R are placed as shown. Find magnetic field at common centre.
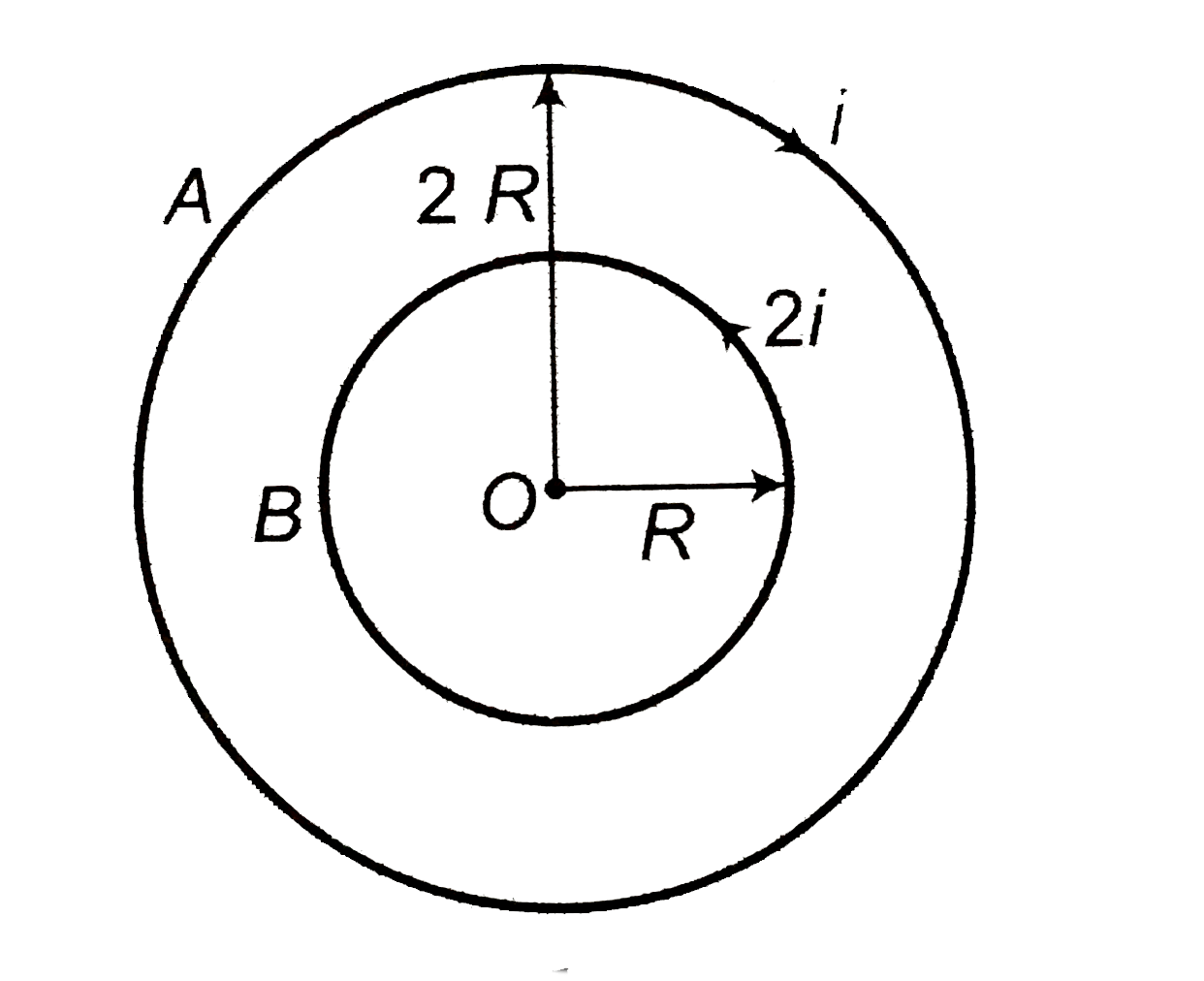
(c) In previous problem, if planes of coil are perpendicular to each other, find magnetic field at common centre.
(d) A charge q distributed uniformely over a circular ring of radius R. The ring rotates about its axis with an angular velocity ω. find the magnetic field (a) at centre and (b) at distance √3R from centre, along the axis.
View SolutionThe magnetic field at the centre of the current carrying coil
View Solution
Knowledge Check
At what distance on the axis, from the centre for circular current carrying coil of radius r, the magnetic field becomes 1/8 th of the magnetic field at centre?
A√2rB23/2rC√3rD3√2rThe magnetic field at the centre of a circular current carrying coil of radius r is Be. The magnetic on its axis at a distance r from the centre is Ba. The value of Be:Ba will be :
A1 : √2B1 : 2√2C2√2 : 1D√2 : 1What is the magnetic field at a distance R from a coil of radius r carrying current l ?
Aμ0lR22(R2+r2)32Bμ0lr22(R2+r2)32Cμ0l2rDμ0l2R
The ratio of the magnetic field at the centre of a current carrying circular wire and the magnetic field at the centre of a semi-circular coil made from the same length of wire will be
View SolutionThe ratio of the magnetic field at the centre of a current carrying circular wire and the magnetic field at the centre of a square coil made from the same length of wire will be
View SolutionThe magnetic field at the centre of current carrying coil is
View SolutionThe ratio of the magnetic field at the centre of a current carrying coil of the radius a and at distance 'a' from centre of the coil and perpendicular to the axis of coil is
View SolutionMagnetic field at the centre of a circular coil of radius R due to curent i flowing through it is B. The magnetic field at a point along the axis at distance R from the centre is :
View Solution
