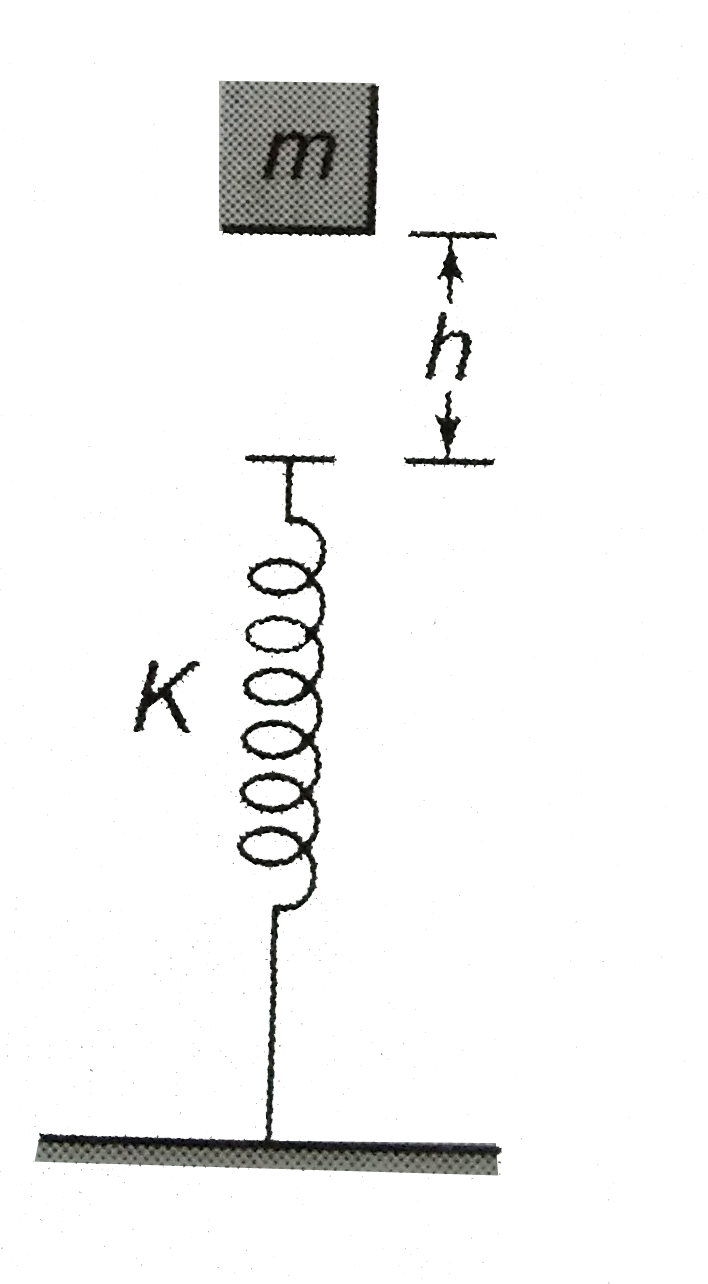If one end of vertical spring is connected to ground and other end is connected to horizontal platform at rest. If a ball of mass m is dropped on it from height h above platform compresses spring by h/2. If h= 10cm then find k
To solve the problem, we need to analyze the situation where a ball of mass m is dropped from a height h onto a spring that compresses by h2. Given that h=10cm, we want to find the spring constant k.
1. Identify the Initial Potential Energy of the Ball:
The ball is dropped from a height h above the platform. The potential energy (PE) of the ball at height h is given by:
PE=mgh
where g is the acceleration due to gravity.
2. Calculate the Height of the Ball from the Reference Point:
When the ball is dropped, it falls a distance h and compresses the spring by h2. Thus, the height from the reference point (the ground) when the ball is at maximum compression is:
Height from reference=h+h2=3h2
3. Calculate the Potential Energy at Maximum Compression:
The potential energy of the ball just before it hits the spring (at height 3h2) is:
PE=mg(3h2)
4. Energy Conservation:
At maximum compression of the spring, all the potential energy of the ball is converted into the elastic potential energy stored in the spring. The elastic potential energy (EPE) in the spring when compressed by h2 is given by:
EPE=12kx2
where x=h2. Therefore:
EPE=12k(h2)2=12kh24=kh28
5. Set the Potential Energy Equal to the Elastic Potential Energy:
By the conservation of energy, we equate the potential energy of the ball to the elastic potential energy of the spring:
mg(3h2)=kh28
6. Rearranging the Equation to Solve for k:
Rearranging the equation gives:
k=8mg(3h2)h2
Simplifying further:
k=12mgh
7. Substituting the Known Values:
Given h=10cm=0.1m, we can substitute this into the equation for k:
k=12mg0.1
8. Final Expression for k:
Since g is approximately 10m/s2:
k=12m⋅100.1=1200mN/m
Conclusion:
The spring constant k is given by:
k=1200mN/m
The ball is dropped from a height h above the platform. The potential energy (PE) of the ball at height h is given by:
PE=mgh
where g is the acceleration due to gravity.
When the ball is dropped, it falls a distance h and compresses the spring by h2. Thus, the height from the reference point (the ground) when the ball is at maximum compression is:
Height from reference=h+h2=3h2
The potential energy of the ball just before it hits the spring (at height 3h2) is:
PE=mg(3h2)
At maximum compression of the spring, all the potential energy of the ball is converted into the elastic potential energy stored in the spring. The elastic potential energy (EPE) in the spring when compressed by h2 is given by:
EPE=12kx2
where x=h2. Therefore:
EPE=12k(h2)2=12kh24=kh28
By the conservation of energy, we equate the potential energy of the ball to the elastic potential energy of the spring:
mg(3h2)=kh28
Rearranging the equation gives:
k=8mg(3h2)h2
Simplifying further:
k=12mgh
Given h=10cm=0.1m, we can substitute this into the equation for k:
k=12mg0.1
Since g is approximately 10m/s2:
k=12m⋅100.1=1200mN/m
The spring constant k is given by:
k=1200mN/m
Topper's Solved these Questions
Similar Questions
Knowledge Check

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2
Given figure shows a massless platform kept on a light elastic spring attached to ground from one end .
A small particle of mass 0.2 kg is dropped on the paltform from a height of 0.26 m , which causes a compression of 0.01 m in the spring . Calculate the height from which the particle must be dropped in order to cause a compressin of 0.05 m .
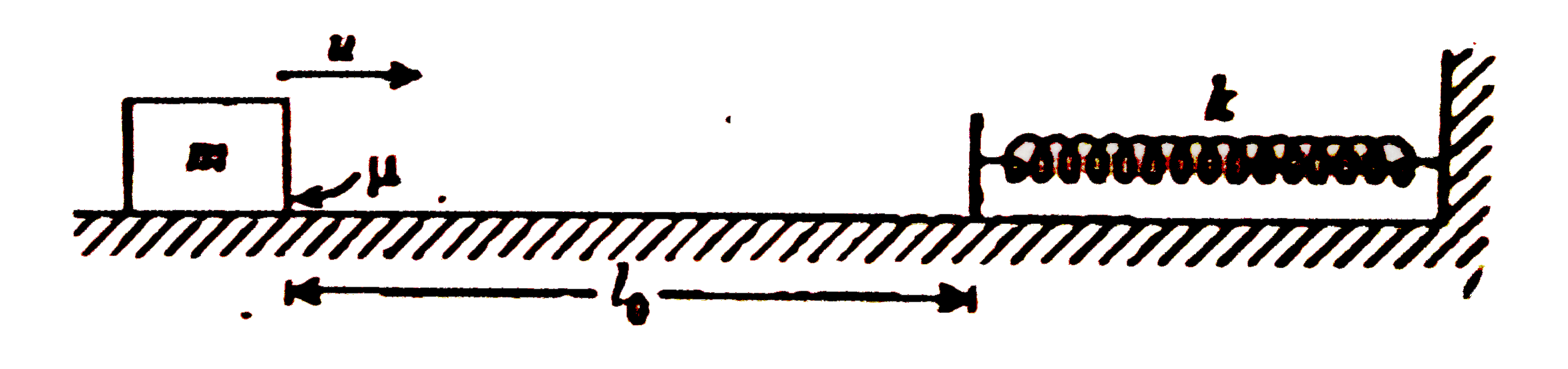
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
View SolutionA man of height h0=2m is bungee jumping from a platform situated at a height h = 25 m above a lake One end of an elastic rope is attached to his foot and the other end is fixed to the platform He starts falling from rest in vertical position. The length and elastic properties of the rope are chosen so that his speed will have been reduced to zero at instant when his head reaches the surface of water. Ultimetely the jumper is hanging from the rope with his head 8m above the water. Find the maxima acceleration acheived during the jump in m/s2)

View SolutionIn Fig. three identical massless springs are kept horizontal. The left end of the first is tied to a wall. The left end of the second spring is tied to a block of mass m placed on rough ground and the ,eft end of the third spring is tied to a block of mass m placed frictionless ground. The right end of each spring is pulled by a force that is increased gradually from zero to F. Extensions in these springs are x1, x2 and x3, respectively. Find the relationship between x1, x2, and x3

View SolutionA small mass 'm' is sliding down on a smooth curved incline form a height 'h' and finally moves through a horizontal smooth surface. A light spring of force constant K is fixed with a vertical rigid stand on the horizontal surface, as shown in the figure. Find the value for the maximum compression in the spring if mass 'm' is released from rest from height 'h' and hits the spring in the horizontal surface.
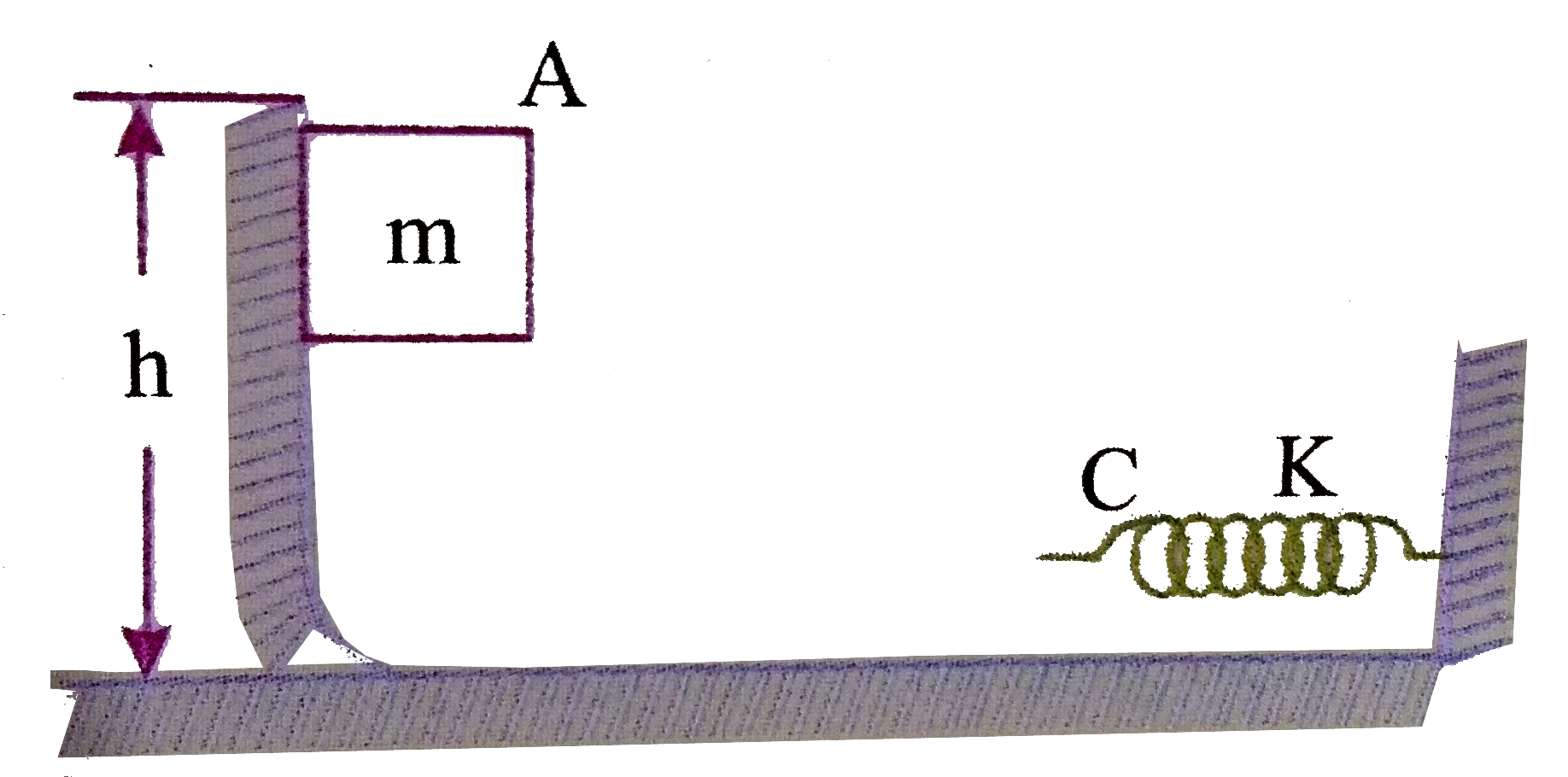 .
.
View SolutionA spring is connected with plank and other end of spring is connected with a block of mass m. initially spring is stretched by a distance x0 and block is connected with a thread which is connected to other end of the plank as shown. If thread is cut, what will be maximum speed of the plank.

View SolutionIn the arrangement shown in the fig. the pulley, the spring and the thread are ideal. The spring is stretched and the two blocks are in contact with a horizontal platform P. When the platform is gradually moved up by 2 cm the tension in the string becomes zero. If the platform is gradually moved down by 2 cm from its original position one of the blocks lose contact with the platform. Given M = 4 kg, m = 2 kg.
(a) Find the force constant (k) of the spring
(b) If the platform continues to move down after one of the blocks loses contact, will the other block also lose contact? Assume that that the platform moves very slowly.

View Solution