A block is projected over a rough surface with speed 9.8 m/s. If friction coefficient of surface block interface is 0.5, Find distance after which block stops.
4.9 m
9.8 m
14.7 m
19.6 m
To solve the problem of finding the distance after which the block stops when projected over a rough surface, we can follow these steps:
1. Identify the Given Values:
- Initial speed of the block, u=9.8m/s
- Coefficient of friction, μ=0.5
- Acceleration due to gravity, g=9.8m/s2
2. Calculate the Frictional Force:
The frictional force Fk acting on the block can be calculated using the formula:
Fk=μ⋅N
where N is the normal force. Since the block is on a horizontal surface, the normal force N is equal to the weight of the block mg:
N=mg
Therefore, the frictional force becomes:
Fk=μ⋅mg=0.5⋅mg
3. Determine the Acceleration:
The acceleration a (which acts as retardation in this case) can be found using Newton's second law:
F=ma
The net force acting on the block due to friction is Fk, thus:
ma=0.5⋅mg
Dividing both sides by m (mass of the block):
a=0.5g=0.5⋅9.8=4.9m/s2
Since this is a deceleration, we will consider it as a=−4.9m/s2.
4. Use the Equation of Motion:
We can use the third equation of motion to find the distance s the block travels before coming to a stop:
v2=u2+2as
Here, the final velocity v=0 (since the block stops), the initial velocity u=9.8m/s, and a=−4.9m/s2. Plugging in the values:
0=(9.8)2+2(−4.9)s
Rearranging gives:
(9.8)2=2⋅4.9⋅s
96.04=9.8s
Solving for s:
s=96.049.8=9.8m
5. Conclusion:
The distance after which the block stops is s=9.8m.
- Initial speed of the block, u=9.8m/s
- Coefficient of friction, μ=0.5
- Acceleration due to gravity, g=9.8m/s2
The frictional force Fk acting on the block can be calculated using the formula:
Fk=μ⋅N
where N is the normal force. Since the block is on a horizontal surface, the normal force N is equal to the weight of the block mg:
N=mg
Therefore, the frictional force becomes:
Fk=μ⋅mg=0.5⋅mg
The acceleration a (which acts as retardation in this case) can be found using Newton's second law:
F=ma
The net force acting on the block due to friction is Fk, thus:
ma=0.5⋅mg
Dividing both sides by m (mass of the block):
a=0.5g=0.5⋅9.8=4.9m/s2
Since this is a deceleration, we will consider it as a=−4.9m/s2.
We can use the third equation of motion to find the distance s the block travels before coming to a stop:
v2=u2+2as
Here, the final velocity v=0 (since the block stops), the initial velocity u=9.8m/s, and a=−4.9m/s2. Plugging in the values:
0=(9.8)2+2(−4.9)s
Rearranging gives:
(9.8)2=2⋅4.9⋅s
96.04=9.8s
Solving for s:
s=96.049.8=9.8m
The distance after which the block stops is s=9.8m.
Topper's Solved these Questions
Similar Questions
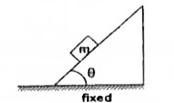
A block of mass m is at rest over the rough surface of the fixed wedge.

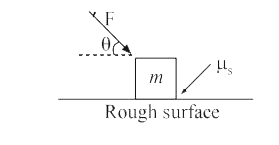
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
View Solution
Knowledge Check
In the figure, a block of weight 60N is placed on a rough surface. The coefficient of friction between the block and the surface is 0.5 . What should be the weight W such that the block does not slip on the surface?
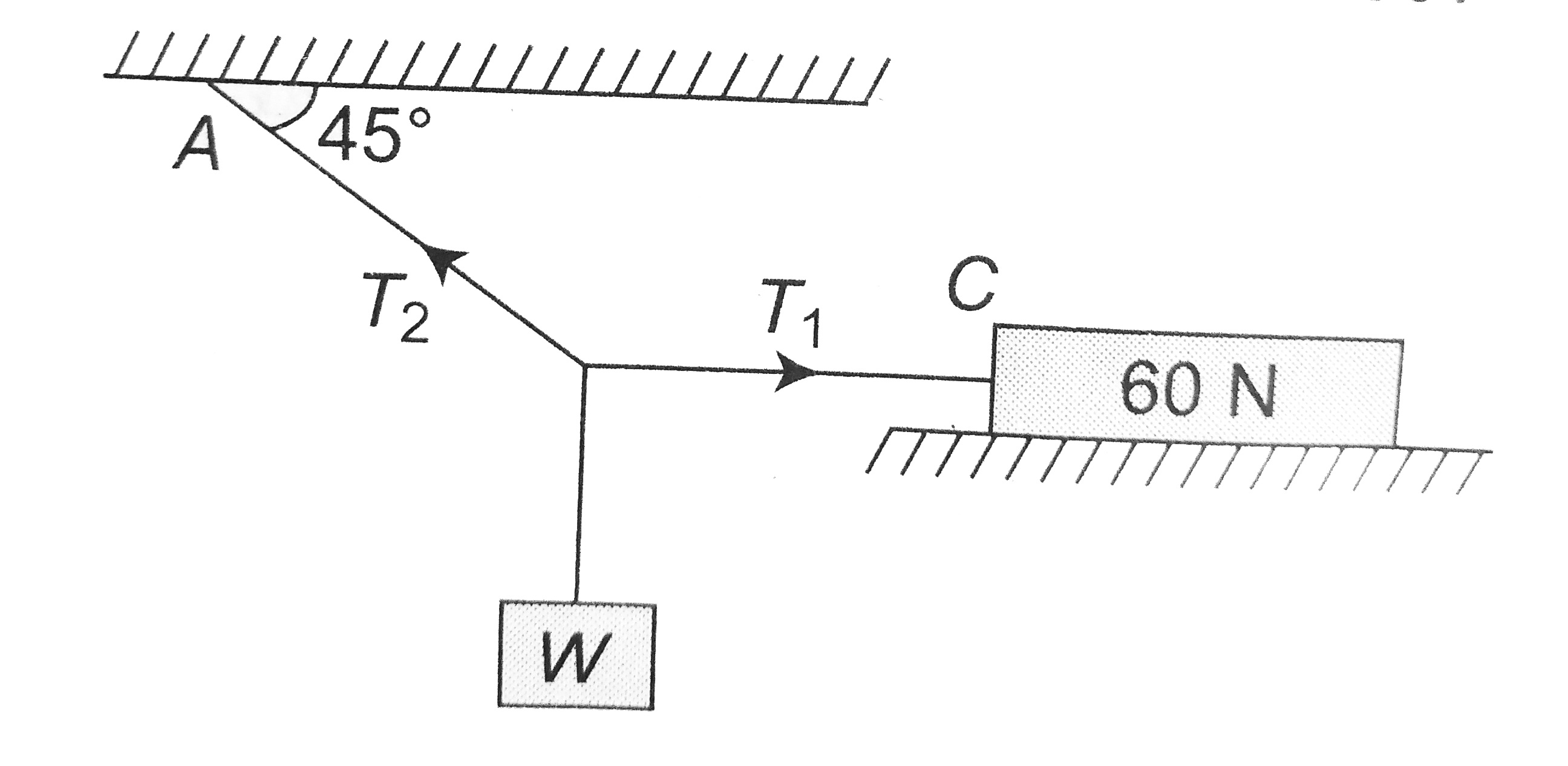 A60NB60√2NC30ND30√2N
A60NB60√2NC30ND30√2NA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
ApmgBμpmgCpμmgDpN2/mgA body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is
Ag2√2Bg2C3g2√2Dg√2
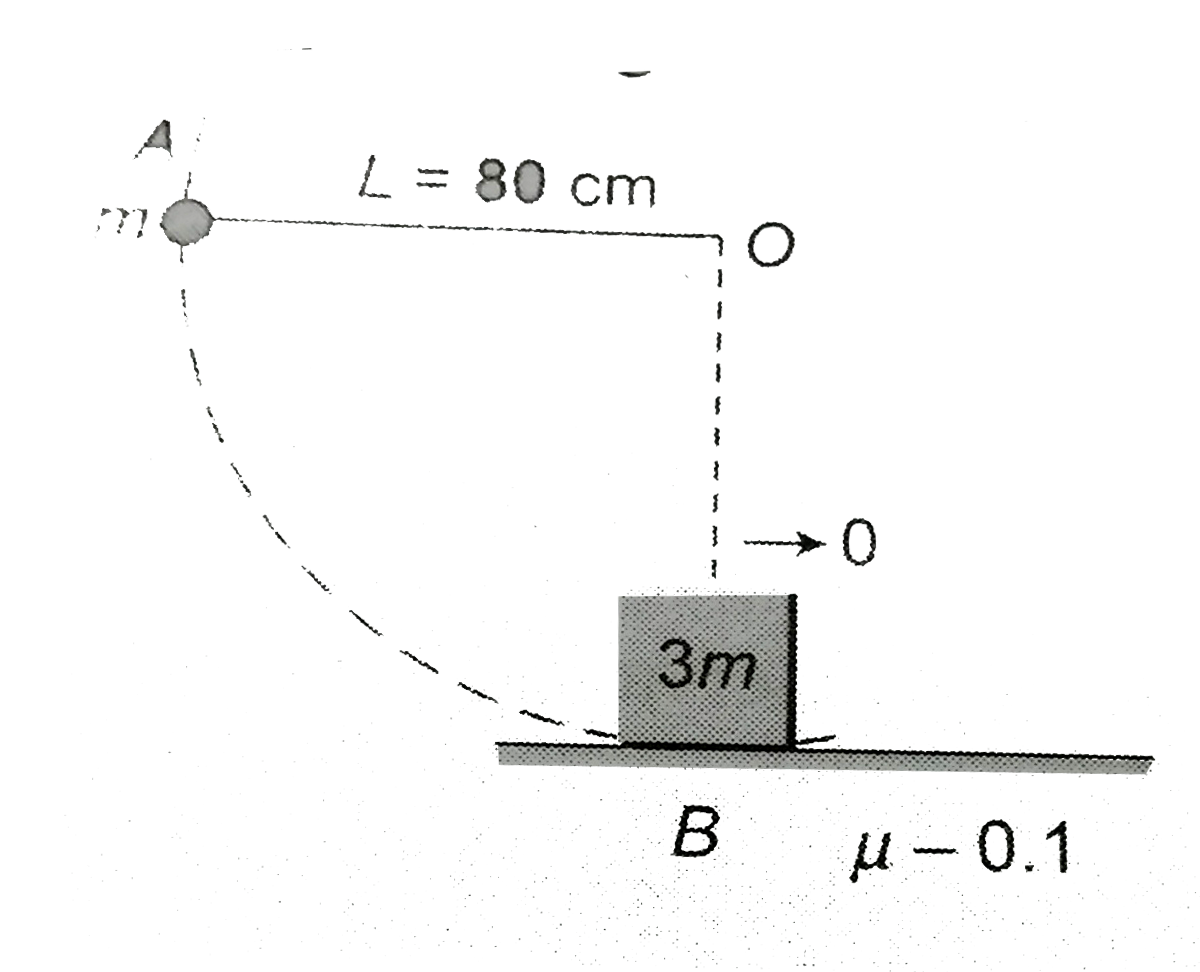
The ball A of mass m is released when the string is horizontal. It strikes a block B of mass 3m kept on a rough surface of friction coefficient μ=0.1. If a head on elastic collision takes place , find the maximum distance travelled by the block on a rough surface.
View SolutionA block of height h is projected along a rough surface of coefficient of friction μ. Find the point of application of the normal force on the block for μk=0.5.
View SolutionA rectangular block is kept on a rough horizontal surface and given some initial velocity. The coefficient of friction between the block and the surface is constant. The block will topple
View SolutionA block placed on a rough harizontal surface is imparted a velocity of 10 m/s. the coefficient of kinetic friction between the block and the surface is 0.5 and g=10m/s2. How much distance the block will cover, before coming to rest?
View SolutionA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View Solution
