Find vA−vB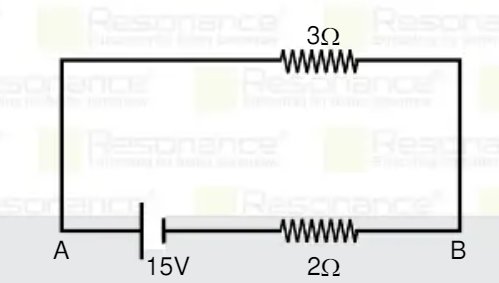 
3V
7V
9V
11V
Step by step video & image solution for Find v_A - v_B by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
1μC charge is shifted from A to B, and it is found that work done by an external force is 40μJ. In doing so against electrostatic forces, find potential difference VA−VB.
View SolutionFind out the following
a. VA−VB
b. VB−VC
c. VC−VA
d. VD−VC
e. VA−VD
f. Arrange the order of potential for points (A, B,C and D).
.View Solution
Knowledge Check
- Question 1 - Select One
In the figure, an ideal flows through the tube, which is of uniform cross-section. The liquid has velocities vA and vB and pressures pA and pB at points A and B respectively.
(i) vA=vB
(ii) vB>vA ltbr gt (iii) pA=pB
(iv) pB>pA.
.A(i),(iii)B(i),(iv)C(ii),(iii)D(ii),(iv) - Question 2 - Select One
In uniform electric field E=10N/C, find
a. VA−VB , b. VB−VCA−10V and 20VB10V and −10VC30V and 20VD−10V and 40V - Question 3 - Select One
In a certain region, electric field E exists along the x - axis which is uniform. Given B=2√3m and BC=4m. Points A, B, and C are in xy plane.
.
Find the potential difference VA−VB between the points AandB.A3 EB4 ECED2 E
The potential difference VA−VB for the circuit shown in fig. is. −(22/x)V. find the value of x.
View SolutionLet V={a,e,i,o,u}and B={a,i,k,u}. Find V−B and B−V
View SolutionAn electric field is expressed as →E=2ˆi+3ˆj. Find the potential difference (VA−VB) between two points A and B whose position vectors are given by rA=ˆi+2ˆjandrB=2ˆi+ˆj+3ˆk.
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
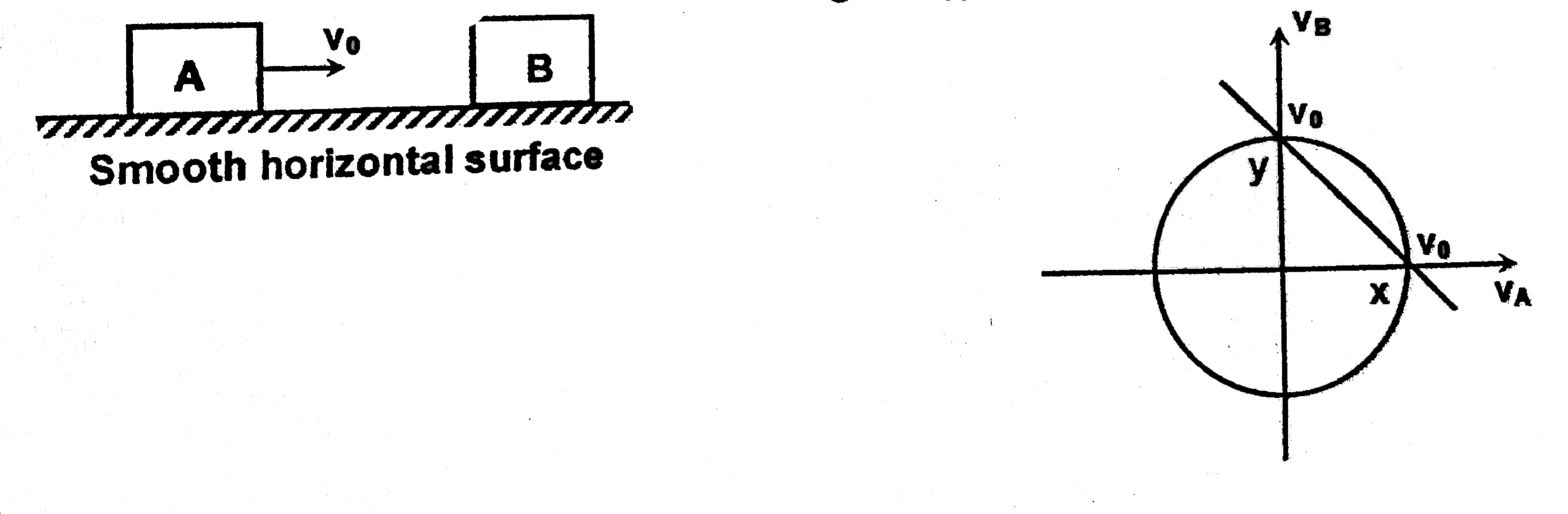
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
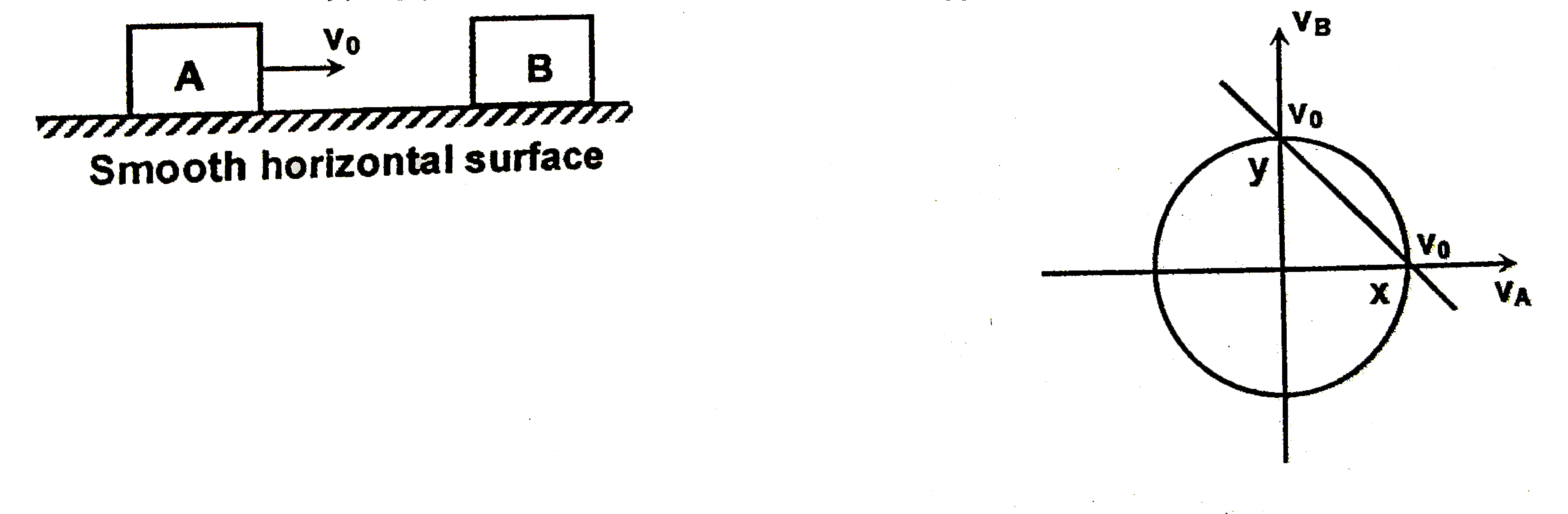
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
If the collision is perfectly inelastic, then the vA−vB plot isView Solution