Two point charges of magnitude Q each are fixed at A and B. At what distance from O (mid point of A and B) should a charge be placed on perpendicular bisector of AB to experience maximum force?
d2
d√2
d2√2
d4
To solve the problem of finding the distance from point O (the midpoint of A and B) at which a charge should be placed on the perpendicular bisector of AB to experience maximum force, we can follow these steps:
Step 1: Understanding the Setup
We have two point charges, each of magnitude Q, fixed at points A and B, separated by a distance d. The point O is the midpoint of AB, and we want to place a charge q at a distance x from O along the perpendicular bisector of AB.
Step 2: Determine the Distances
The distance from the charge q at point O to each charge Q at points A and B can be determined using the Pythagorean theorem. The distance from the charge q to either charge Q is given by:
r=√x2+(d2)2=√x2+d24
Step 3: Calculate the Forces
The force F exerted by each charge Q on the charge q can be calculated using Coulomb's law:
F=kQqr2
Substituting r:
F=kQqx2+d24
Since there are two charges exerting force on q, the total force Fnet acting on q will be the vertical components of the forces due to both charges (as the horizontal components will cancel out):
Fnet=2Fcos(θ)
Step 4: Find the Angle
From the geometry of the situation, we can find cos(θ):
cos(θ)=d2√x2+d24
Step 5: Substitute and Simplify
Substituting F and cos(θ) into the expression for Fnet:
Fnet=2⎛⎜⎝kQqx2+d24⎞⎟⎠⎛⎜
⎜⎝d2√x2+d24⎞⎟
⎟⎠
This simplifies to:
Fnet=kQqd(x2+d24)3/2
Step 6: Maximize the Force
To find the maximum force, we differentiate Fnet with respect to x and set the derivative equal to zero:
ddx⎛⎜⎝kQqd(x2+d24)3/2⎞⎟⎠=0
Using the quotient rule and simplifying, we find the critical points.
Step 7: Solve for x
After differentiating and simplifying, we find:
x=d2√2
Conclusion
The distance from point O at which the charge should be placed to experience maximum force is:
d2√2
We have two point charges, each of magnitude Q, fixed at points A and B, separated by a distance d. The point O is the midpoint of AB, and we want to place a charge q at a distance x from O along the perpendicular bisector of AB.
The distance from the charge q at point O to each charge Q at points A and B can be determined using the Pythagorean theorem. The distance from the charge q to either charge Q is given by:
r=√x2+(d2)2=√x2+d24
The force F exerted by each charge Q on the charge q can be calculated using Coulomb's law:
F=kQqr2
Substituting r:
F=kQqx2+d24
Fnet=2Fcos(θ)
From the geometry of the situation, we can find cos(θ):
cos(θ)=d2√x2+d24
Substituting F and cos(θ) into the expression for Fnet:
Fnet=2⎛⎜⎝kQqx2+d24⎞⎟⎠⎛⎜
⎜⎝d2√x2+d24⎞⎟
⎟⎠
This simplifies to:
Fnet=kQqd(x2+d24)3/2
To find the maximum force, we differentiate Fnet with respect to x and set the derivative equal to zero:
ddx⎛⎜⎝kQqd(x2+d24)3/2⎞⎟⎠=0
Using the quotient rule and simplifying, we find the critical points.
After differentiating and simplifying, we find:
x=d2√2
The distance from point O at which the charge should be placed to experience maximum force is:
d2√2
Topper's Solved these Questions
Similar Questions
Two particles A and B having equal charges are placed at distance d apart. A third charged particle placed on the perpendicular bisector at a distance x will experience the maximum Coulomb’s force when :
View SolutionTwo point charges , −2μC and +6μC are fixed on a table at a distance 10 cm from each other. Where should the third charge be placed so that no net force acts on it ?
View Solution
Knowledge Check
Two equal charges are separated by a distance d. A third charge placed on a perpendicular bisector at x distance will experience maximum coulomb force when
Ax=d√2Bx=d2Cx=d2√2Dx=d2√3Two equal point charges A and B are R distance apart. A third point charge placed on the perpendicular bisector at a disttance d from the centre will experience maximum electrostatic force when
Ad=R2√2Bd=R√2Cd=R√2Dd=2√2 RTwo fixed charges 4Q (positive) and Q (negative) are located at A and Bthe distance AB being 3m
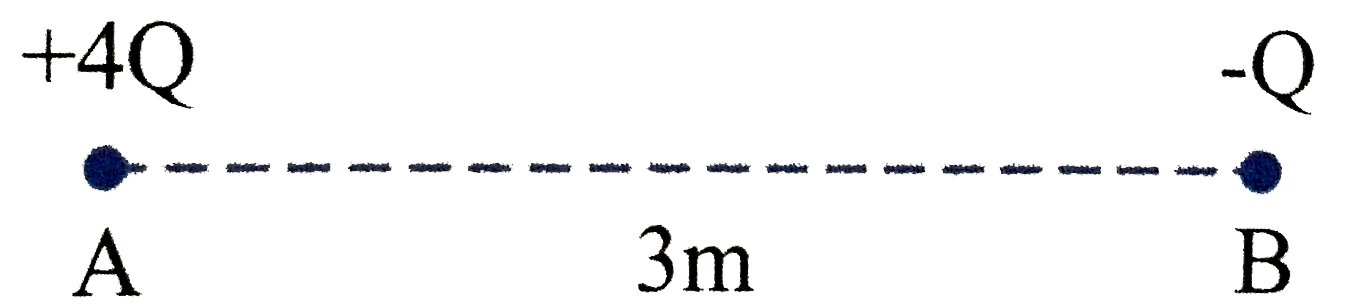 AThe point P where the resultant field due to both is zero is on AB outside ABBThe point P where the resutlant field due to both is zero is on AB inside ABCIf a positive charge is placed at P and displaced slightly along AB it will execute oscillations.DIf a negative charge is placed at P and displaced slightly along AB it will execute oscillations.
AThe point P where the resultant field due to both is zero is on AB outside ABBThe point P where the resutlant field due to both is zero is on AB inside ABCIf a positive charge is placed at P and displaced slightly along AB it will execute oscillations.DIf a negative charge is placed at P and displaced slightly along AB it will execute oscillations.
Two point charge Q and 4Q are fixed at a distance of 12cm from each other. Sketch lines of force and locate the neutral point, if any .
View SolutionTwo fixed point charges +4e and +e units are separated by a distance a. Where should a third point charge be placed for it to be in equilibrium?
View SolutionTwo point charges of 1μCand−1μC are separated by a distance of 100 Å. A point P is at a distance of 10 cm from the midpoint and on the perpendicular bisector of the line joining the two charges. The electric field at P will be
View SolutionTwo charges 10μCand−10μC are placed at points A.andB separated by a distance of 10 cm. Find the electric field at a point P on the perpendicular bisector of AB at. a distance of 12 cm from its middle point.
View SolutionTwo point metal charges−q and +2q are placed at a certain distance apart.Where should a third point charge be placed so that it is in equilibrium?
View Solution
