A block of mass m is kept inside a box. The box is falling down with acceleration is g/4. Find the force exerted by block m on surface of box.
To solve the problem, we need to analyze the forces acting on the block of mass m inside the box that is falling with an acceleration of g/4.
1. Identify the forces acting on the block:
The block of mass m experiences two main forces:
- The gravitational force acting downwards, which is Fg=mg.
- The normal force N exerted by the surface of the box on the block, acting upwards.
2. Determine the effective acceleration:
Since the box is falling with an acceleration of g/4, we need to find the effective acceleration acting on the block relative to the box. The effective acceleration of the block is given by:
aeffective=g−g4=3g4
This is because the block is falling under gravity while the box is also accelerating downwards.
3. Apply Newton's second law:
According to Newton's second law, the net force acting on the block can be expressed as:
Fnet=maeffective=m⋅3g4
4. Set up the equation for the forces:
The net force acting on the block can also be expressed in terms of the normal force and the gravitational force:
N−mg=−maeffective
Substituting aeffective into the equation gives:
N−mg=−m⋅3g4
5. Solve for the normal force N:
Rearranging the equation:
N=mg−m⋅3g4
N=mg−3mg4=4mg4−3mg4=mg4
6. Calculate the force exerted by the block on the surface of the box:
The force exerted by the block on the surface of the box is equal to the normal force N:
N=mg4
Final Answer:
Thus, the force exerted by the block of mass m on the surface of the box is:
mg4
The block of mass m experiences two main forces:
- The gravitational force acting downwards, which is Fg=mg.
- The normal force N exerted by the surface of the box on the block, acting upwards.
Since the box is falling with an acceleration of g/4, we need to find the effective acceleration acting on the block relative to the box. The effective acceleration of the block is given by:
aeffective=g−g4=3g4
This is because the block is falling under gravity while the box is also accelerating downwards.
According to Newton's second law, the net force acting on the block can be expressed as:
Fnet=maeffective=m⋅3g4
The net force acting on the block can also be expressed in terms of the normal force and the gravitational force:
N−mg=−maeffective
Substituting aeffective into the equation gives:
N−mg=−m⋅3g4
Rearranging the equation:
N=mg−m⋅3g4
N=mg−3mg4=4mg4−3mg4=mg4
The force exerted by the block on the surface of the box is equal to the normal force N:
N=mg4
Thus, the force exerted by the block of mass m on the surface of the box is:
mg4
Topper's Solved these Questions
Similar Questions
In the previous problem if M=80kg and m=410kg and the boy pulls the rope such that the system (boy+box) moves upward with acceleration 5m/s2,find the force exerted by the boy and contact force between the boy and the box.
View SolutionA heavy box of mass 20 kg is pulled on a horizontal force.If the coefficient of kinetic friction between the box and the horizontal surface is 0.25, find the force of friction exerted by horizontal surface on the box.
View Solution
Knowledge Check
A block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
AmgBmg sin θCμmgcosθDμmgsinθA box is accelerating with acceleration =20m/s2. A block of mas 10 kg placed inside the box and is in contact with the verticle wall as shown. The friction coefficient between the block and the wall is μ=0.6 and take g=10 m//s^(2)
 AThe acceleration of the block will be 20m/s2BThe friction force acting on the block will be 100 NCThe contact force between the verticle wall and the block will be 100√5 NDThe contact force between the verticle wall and the block is only electromegnetic in nature
AThe acceleration of the block will be 20m/s2BThe friction force acting on the block will be 100 NCThe contact force between the verticle wall and the block will be 100√5 NDThe contact force between the verticle wall and the block is only electromegnetic in natureA hollow cubical box P is moving on a smooth horizontal surface in the x-y plane with constant acceleration of →a=3ˆi+4ˆjm/s2.A block Q of mass 2 kg is at rest inside the cubical box as shown in figure. If the coefficient of friction between the surface of the cube P and the block Q is 0.6. Then the force of friction between P and Q is :
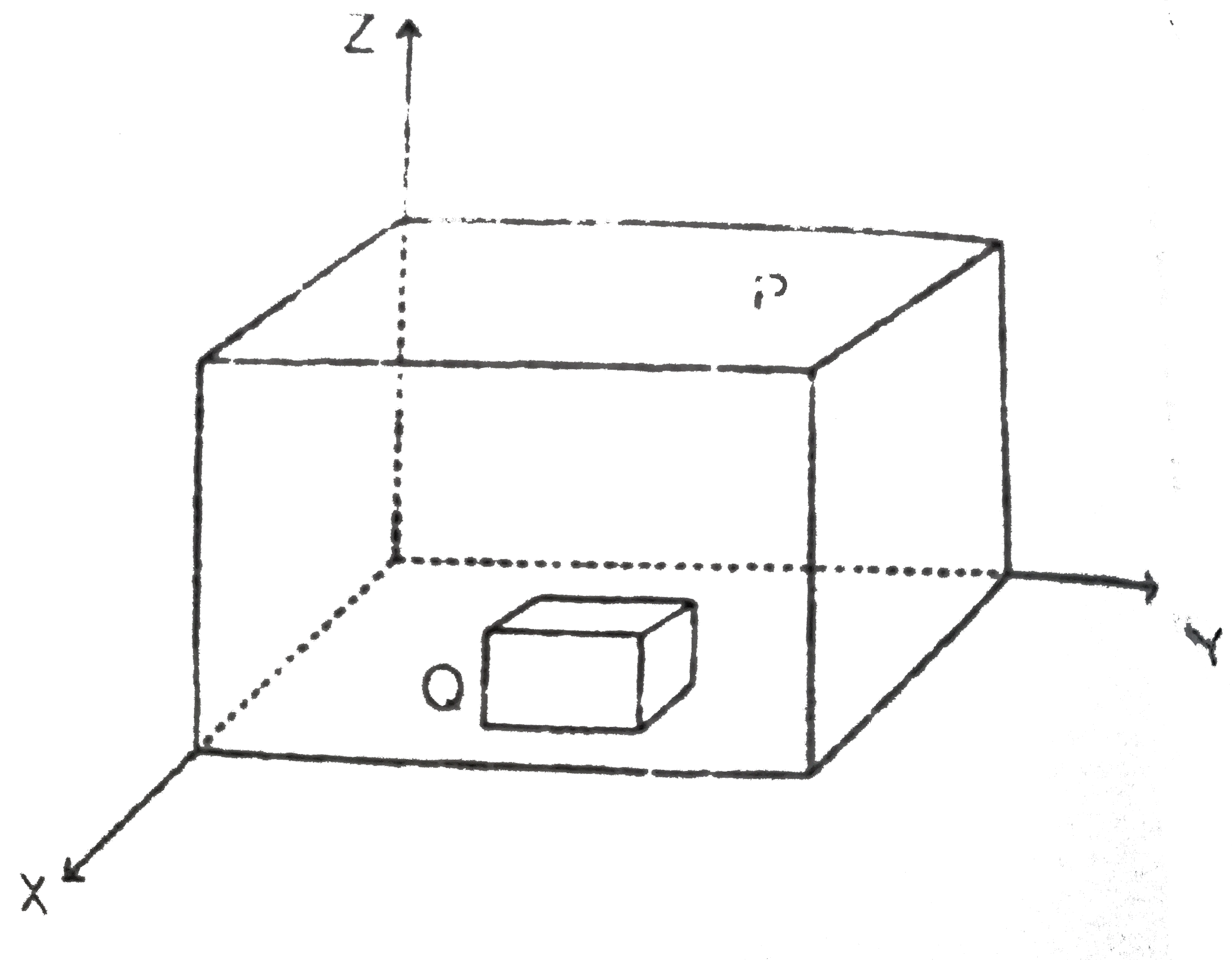 A5 NB8 NC12 ND10 N
A5 NB8 NC12 ND10 N
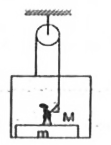
A man of mass M is standing on a plank kept in a box. The plank and box as a whole has mass m. A light string passing over a fixed smooth pulley connects the man and box. If the box remains stationary, find the tension in the string and the force exerted by the man on the plank.
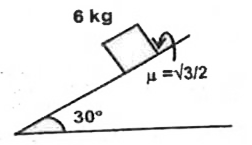
View SolutionA block of mass 6 kg is kept on rough surface as shown in figure. Find acceleration and friction force acting on the block. (Take g=10m/s2)
View SolutionA 2kg box sits on a 3kg box which sits on a 5kg box.The 5kg box rests on a table.What is normal force exerted by 5kg box on the 3kg box?
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionConsider the situation as shown in the figure. The boy of mass M holds the light rope and the system is at rest. If m is mass of the box, find the force exerted by the boy on the rope and contact force beteween the boy and the box.

View Solution
