An infinitely long hollow conducting cylinder with radius R carries a uniform current along its surface.
Choose the correct representation of magnetic field (B) as a function of radial distance (r) from the axis of cylinder.
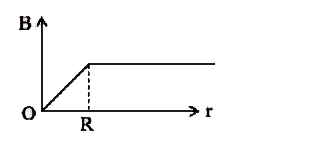


To solve the problem of finding the magnetic field B as a function of radial distance r from the axis of an infinitely long hollow conducting cylinder carrying a uniform current along its surface, we can follow these steps:
Step 1: Understand the Configuration
We have an infinitely long hollow conducting cylinder with radius R that carries a uniform current I along its surface. The current flows uniformly around the cylinder.
Step 2: Apply Ampere's Law
Ampere's Law states that:
∮B⋅dL=μ0Ienc
where Ienc is the current enclosed by the Amperian loop.
Step 3: Analyze the Regions
We need to analyze two regions:
1. Inside the cylinder (r<R)
2. Outside the cylinder (r>R)
Step 4: Magnetic Field Inside the Cylinder (r<R)
For any point inside the hollow conducting cylinder, there is no current enclosed by the Amperian loop since the current flows only on the surface. Thus:
Ienc=0
Applying Ampere's Law:
∮B⋅dL=0⟹B=0for r<R
Step 5: Magnetic Field Outside the Cylinder (r>R)
For points outside the cylinder, we consider a circular Amperian loop of radius r where r>R. The current enclosed by this loop is equal to the total current I flowing on the surface of the cylinder. Thus:
Ienc=I
Applying Ampere's Law:
B⋅(2πr)=μ0I⟹B=μ0I2πrfor r>R
Step 6: Summary of Results
- For r<R: B=0
- For r>R: B=μ0I2πr
Step 7: Graphical Representation
The magnetic field B as a function of r can be represented as:
- B=0 for r<R (a flat line on the x-axis)
- B decreases inversely with r for r>R (a hyperbolic curve)
Conclusion
The correct representation of the magnetic field B as a function of radial distance r from the axis of the cylinder is that it is zero for r<R and inversely proportional to r for r>R.
We have an infinitely long hollow conducting cylinder with radius R that carries a uniform current I along its surface. The current flows uniformly around the cylinder.
Ampere's Law states that:
∮B⋅dL=μ0Ienc
where Ienc is the current enclosed by the Amperian loop.
We need to analyze two regions:
1. Inside the cylinder (r<R)
2. Outside the cylinder (r>R)
For any point inside the hollow conducting cylinder, there is no current enclosed by the Amperian loop since the current flows only on the surface. Thus:
Ienc=0
Applying Ampere's Law:
∮B⋅dL=0⟹B=0for r<R
For points outside the cylinder, we consider a circular Amperian loop of radius r where r>R. The current enclosed by this loop is equal to the total current I flowing on the surface of the cylinder. Thus:
Ienc=I
Applying Ampere's Law:
B⋅(2πr)=μ0I⟹B=μ0I2πrfor r>R
- For r<R: B=0
- For r>R: B=μ0I2πr
The magnetic field B as a function of r can be represented as:
- B=0 for r<R (a flat line on the x-axis)
- B decreases inversely with r for r>R (a hyperbolic curve)
The correct representation of the magnetic field B as a function of radial distance r from the axis of the cylinder is that it is zero for r<R and inversely proportional to r for r>R.
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section B
10 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS
60 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics -Section A
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
Knowledge Check
An infinitely long hollow conducting cylinder with inner radius r2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
A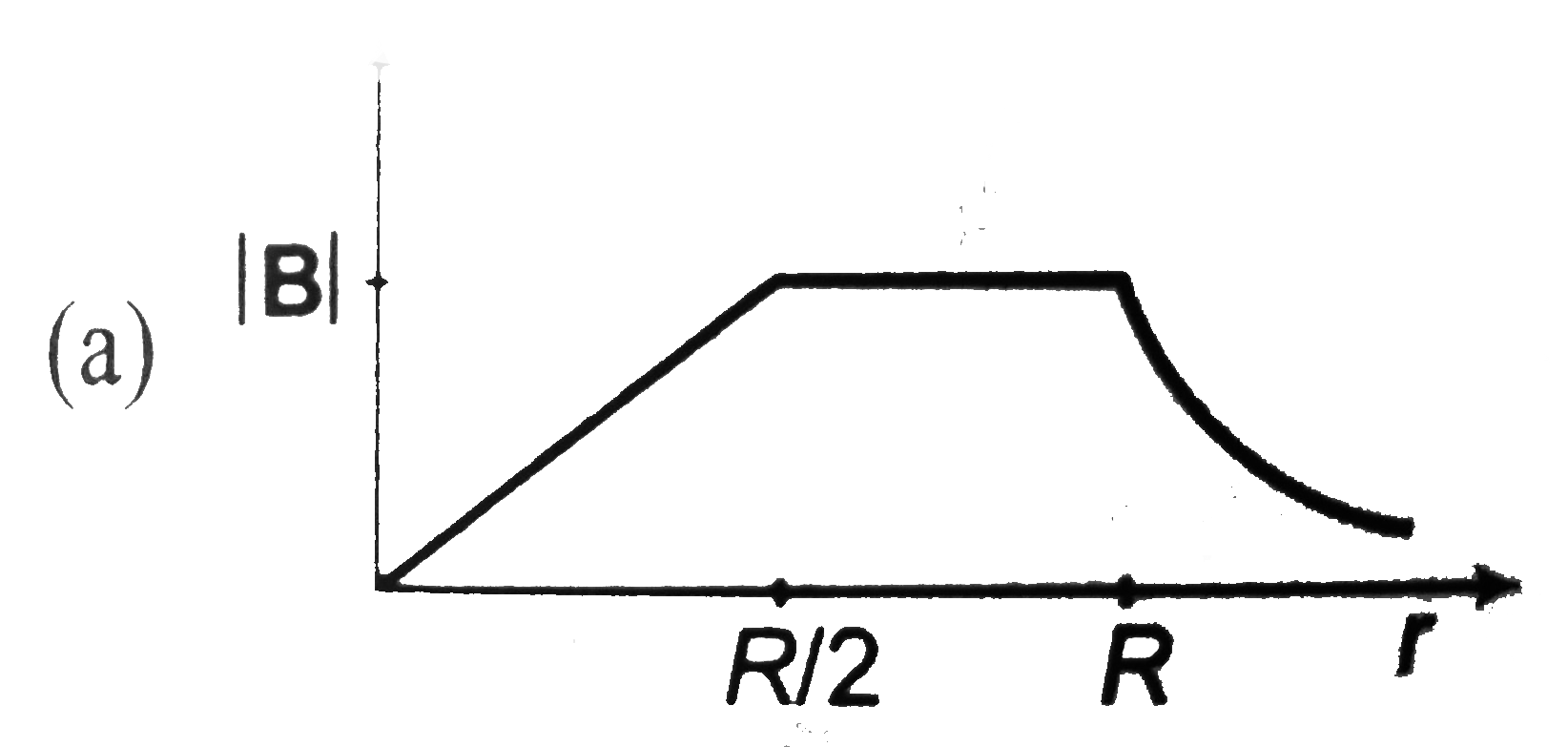 B
B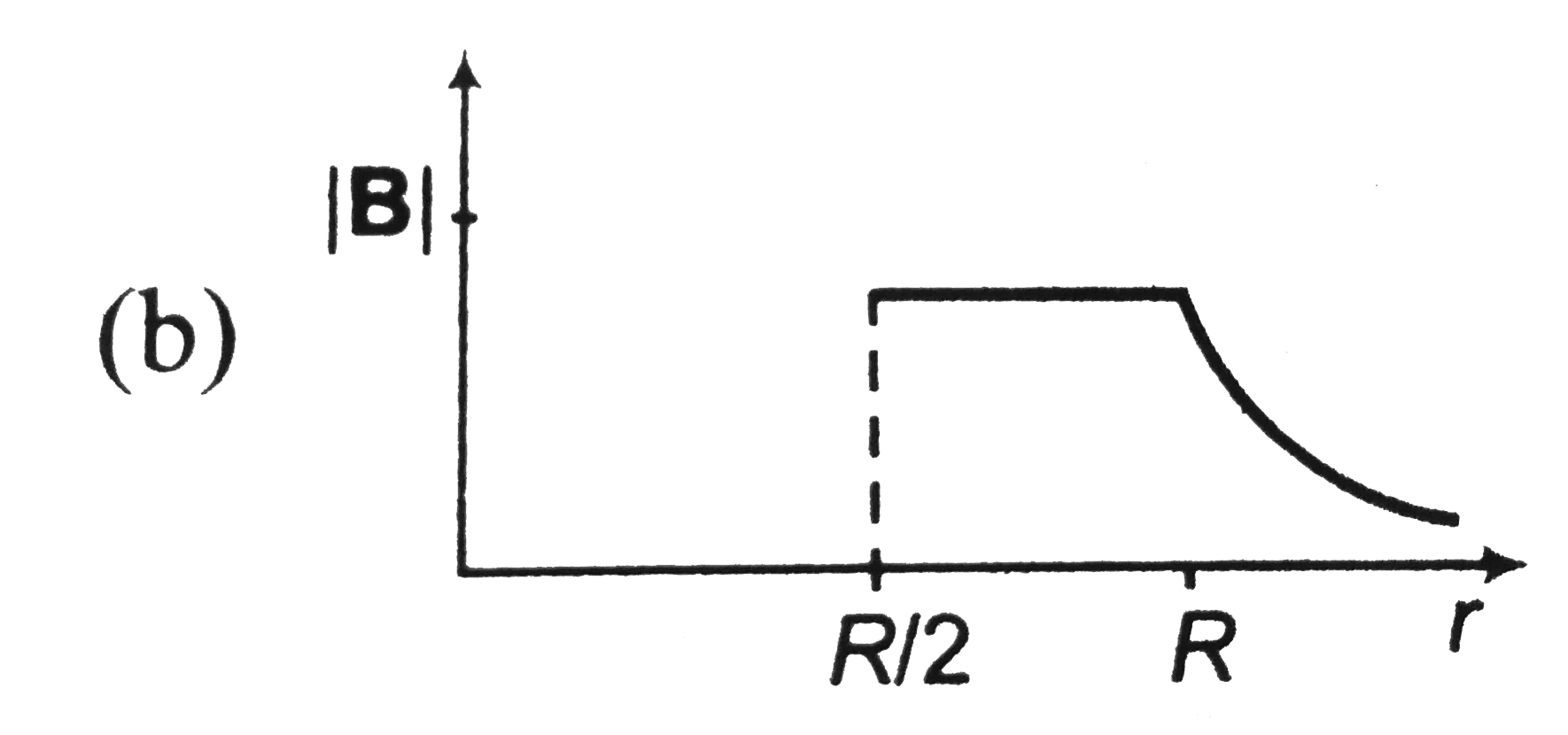 C
C D
D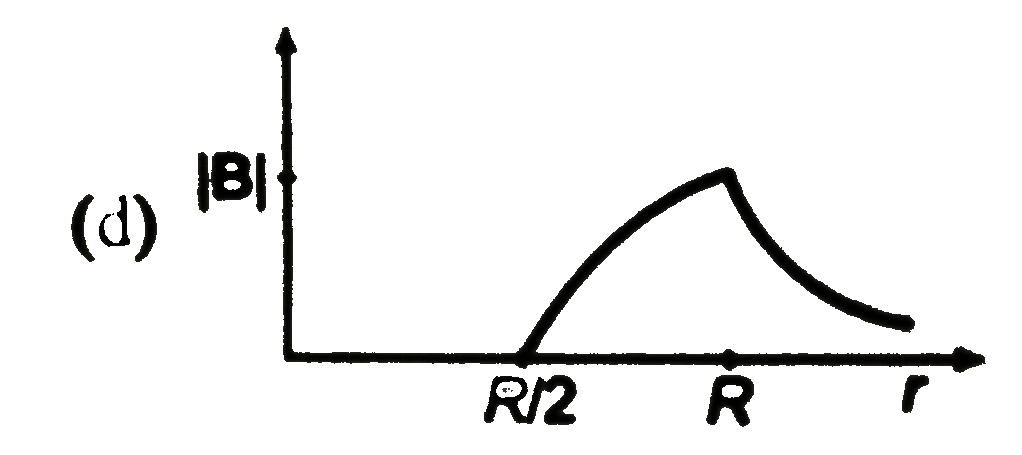
An infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
A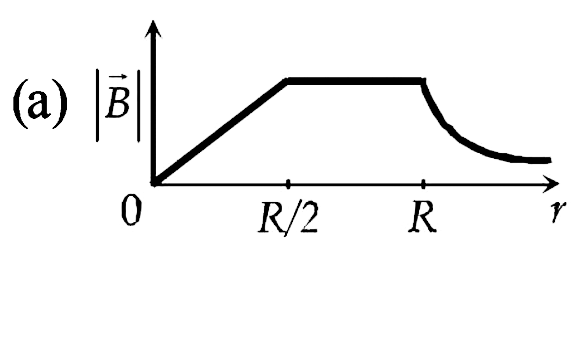 B
B C
C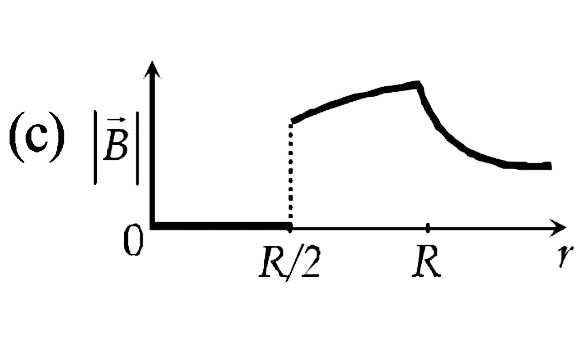 D
D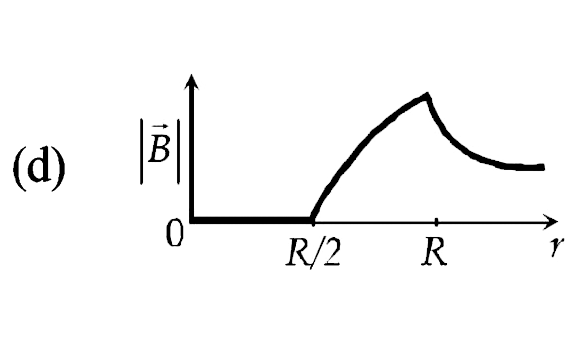
A long cylinder of wire of radius 'a' carries a current i distributed uniformly over its cross section. If the magnetic fields at distances r<aandR>a from the axis have equal magnitude, then
Aa=R+r2Ba=√ReCa=Rr/(R+r)Da=R2/r
A thick current carrying cable of radius 'R' carries current 'I' uniformly distributed across its crosssection. The variation of magnetic field B(r) due to cable with distance 'r' from the axis of the cable is represented by.
View SolutionA thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionA long straight conducting solid cylindrical wire of radius R carries a steady current / that is uniformly distributed throughout the cross section of the wire. Choose the correct graph of magnetic field B versus r (where r is distance from the axis of the wire)
View SolutionMoment of inertia of a hollow cylinder of mass M and radius R, about the axis of cylinder is
View SolutionFigure shows the cross-sectional view of the hollow cylindrical conductor with inner radius 'R' and outer radius '2R', cylinder carrying uniformly distributed current along it's axis. The magnetic induction at point 'P' at a distance 3R2 from the axis of the cylinder will be
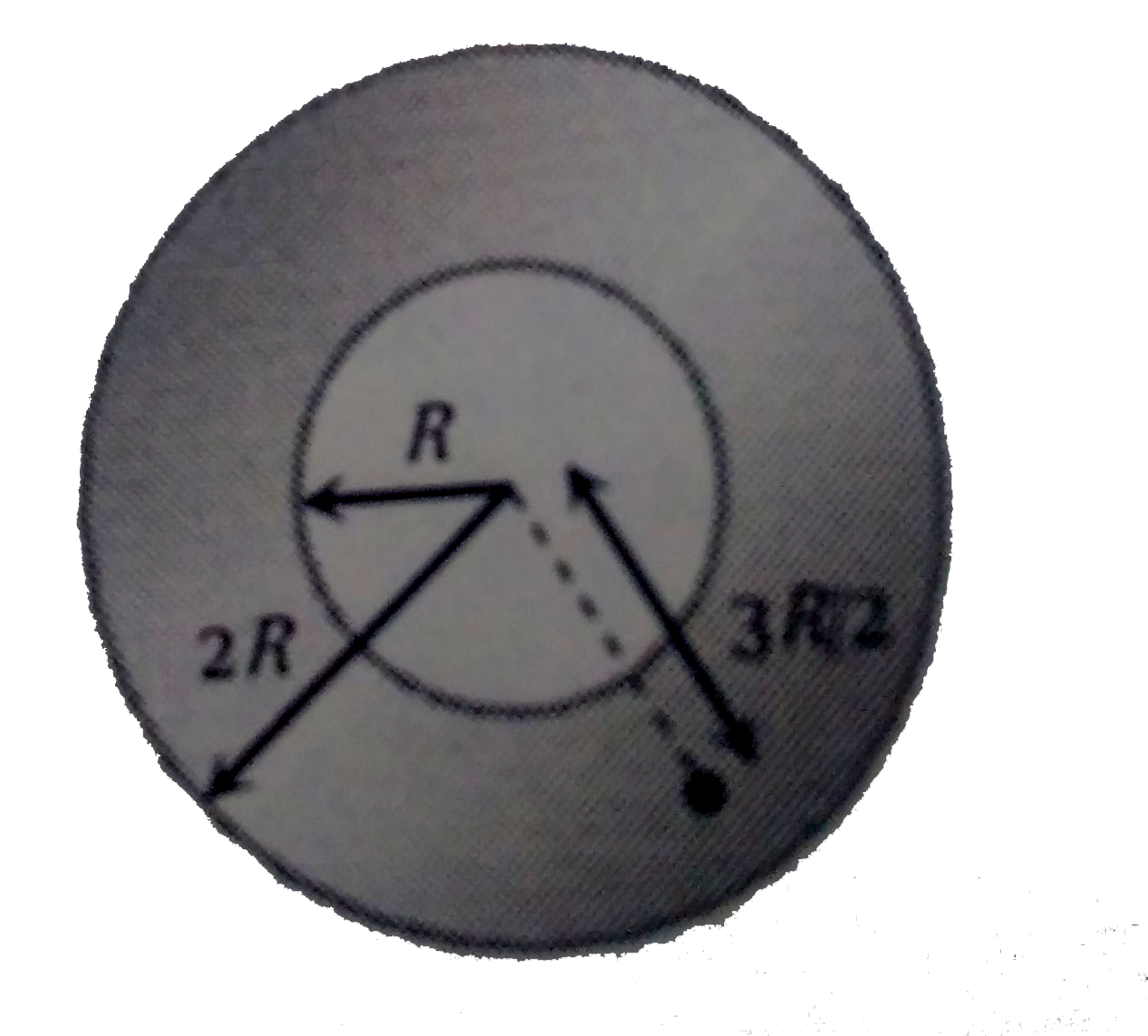
View Solution
