Given below are two statements :
Statement- I : When µ mnount of an ideal gas undergoes adiabatic change from state (P1,V1,T1) to state (P2,V2,T2), then work done is W=μR(T2−T1)1−γ where γ=CpCv and R=universal gas constant.
Statement - II : In the above case, when work is done on the gas the temperature of the gas would rise.
Choose the correct answer from the options given below :
Both statement-I and statement-II are true.
Both statement-I and statement-II are false.
Statement-I is true but statement-II is false.
Statement-I is false but statement-II is true.
To solve the problem, we need to analyze both statements provided in the question regarding the adiabatic process of an ideal gas.
1. Understanding Adiabatic Process:
- In an adiabatic process, there is no heat exchange with the surroundings (Q = 0). The change in internal energy (ΔU) is equal to the work done (W) on or by the gas.
- The first law of thermodynamics states:
Q=ΔU+W
For an adiabatic process, this simplifies to:
0=ΔU+W⟹ΔU=−W
2. Work Done in Adiabatic Process:
- The work done by the gas during an adiabatic process can be expressed as:
W=nR(T2−T1)1−γ
where γ=CpCv and R is the universal gas constant.
3. Analyzing Statement I:
- Statement I claims that the work done during the adiabatic change is given by the formula W=nR(T2−T1)1−γ.
- This statement is true based on the derivation of work done in an adiabatic process.
4. Analyzing Statement II:
- Statement II states that if work is done on the gas, the temperature of the gas would rise.
- When work is done on the gas (W is negative), the internal energy increases, leading to an increase in temperature (ΔU is positive). Therefore, if work is done on the gas, the temperature indeed rises.
5. Conclusion:
- Both statements are true. However, they are related but not dependent on each other. Thus, the conclusion is that both statements are true.
Final Answer:
Both Statement I and Statement II are true.
- In an adiabatic process, there is no heat exchange with the surroundings (Q = 0). The change in internal energy (ΔU) is equal to the work done (W) on or by the gas.
- The first law of thermodynamics states:
Q=ΔU+W
For an adiabatic process, this simplifies to:
0=ΔU+W⟹ΔU=−W
- The work done by the gas during an adiabatic process can be expressed as:
W=nR(T2−T1)1−γ
where γ=CpCv and R is the universal gas constant.
- Statement I claims that the work done during the adiabatic change is given by the formula W=nR(T2−T1)1−γ.
- This statement is true based on the derivation of work done in an adiabatic process.
- Statement II states that if work is done on the gas, the temperature of the gas would rise.
- When work is done on the gas (W is negative), the internal energy increases, leading to an increase in temperature (ΔU is positive). Therefore, if work is done on the gas, the temperature indeed rises.
- Both statements are true. However, they are related but not dependent on each other. Thus, the conclusion is that both statements are true.
Both Statement I and Statement II are true.
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section B
10 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS
60 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics -Section A
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
Knowledge Check
If a system undergoes an adiabatic change from state 1 to state 2, the work done by the gas is:
AU1−U2BU2−U1CCV(T2−T2)D12(P1V2−P1V1)Ideal gas undergoes an adiabatic change in its state from (P1V1,T1) to(,P2,V2T2). The work done (W) in the process is (n = number of moles, Cp and Cv are molar specific heats of gas)
AW=n(T1−T2)CPBW=n(T1−T2)CvCW=n(T1+T2)CpDW=n(T1+T2)CVAn ideal monatomic gas expands in such a way that TV12= constant, where T and V are the temperature & volume of the gas, choose the correct option(s)
AThe molar heat capacity is C=CV−2RBThe internal energy of gas decreases.CTemperature of gas decreases.DPressure of gas increases.
The change in the entropy of a 1 mole of an ideal gas which went through an isothermal process form an initial state (P1,V1,T) to the final state (P2,V2<T) is equal to
View SolutionAn ideal gas is transformed from state A(P1,V1) to the state B(P2,V2) through path AB. In this process the work done by the gas is
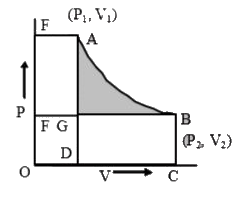
View SolutionA gas expands under constant pressure P from volume V1 toV2The work done by the gas is
View SolutionIn an adiabatic process, the state of a gas is changed from P1,V1,T1,toP2,V2,T2. Which of the following relation is correct
View SolutionOne mole of an ideal gas at temperature T1 expends according to the law PV2=a (constant). The work done by the gas till tempereature of gas becomes T2 is
View Solution