The terminal velocity (vt) of the spherical rain drop depends on the radius (r) of the spherical rain drop as:
r1/2
r
r2
r3
The correct Answer is:C
To determine how the terminal velocity vt of a spherical raindrop depends on its radius r, we can use the formula for terminal velocity derived from Stokes' law. The terminal velocity of a sphere falling through a viscous fluid is given by:
vt=29⋅gr2(ρb−ρl)η
Where:
- vt = terminal velocity
- g = acceleration due to gravity
- r = radius of the raindrop
- ρb = density of the raindrop (body)
- ρl = density of the fluid (liquid)
- η = coefficient of viscosity of the fluid
1. Identify the Variables:
- The terminal velocity vt depends on the radius r of the raindrop, the gravitational acceleration g, the densities ρb and ρl, and the viscosity η.
2. Write the Formula:
- The formula for terminal velocity is given as:
vt=29⋅gr2(ρb−ρl)η
3. Analyze the Dependence on Radius:
- From the formula, we can see that vt is proportional to r2. This means that if the radius r of the raindrop increases, the terminal velocity vt increases with the square of the radius.
4. Conclusion:
- Therefore, we conclude that the terminal velocity vt of a spherical raindrop depends on the square of its radius r.
Final Expression:
vt∝r2
- vt = terminal velocity
- g = acceleration due to gravity
- r = radius of the raindrop
- ρb = density of the raindrop (body)
- ρl = density of the fluid (liquid)
- η = coefficient of viscosity of the fluid
- The terminal velocity vt depends on the radius r of the raindrop, the gravitational acceleration g, the densities ρb and ρl, and the viscosity η.
- The formula for terminal velocity is given as:
vt=29⋅gr2(ρb−ρl)η
- From the formula, we can see that vt is proportional to r2. This means that if the radius r of the raindrop increases, the terminal velocity vt increases with the square of the radius.
- Therefore, we conclude that the terminal velocity vt of a spherical raindrop depends on the square of its radius r.
vt∝r2
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PART : PHYSICS30videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)20videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section B10videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )10videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question360videos
JEE MAINS 2023 JAN ACTUAL PAPER
Similar Questions
Knowledge Check
- Question 1 - Select One
Terminal velocity (V) of a spherical object varies with a radius of object (r) -
A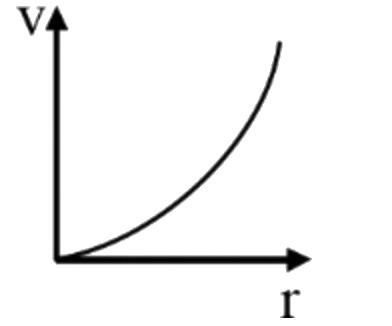 B
B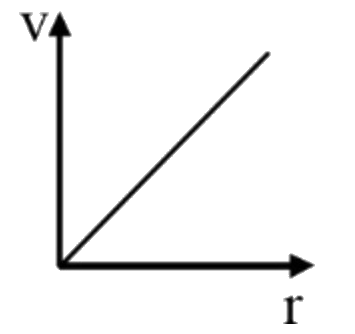 C
C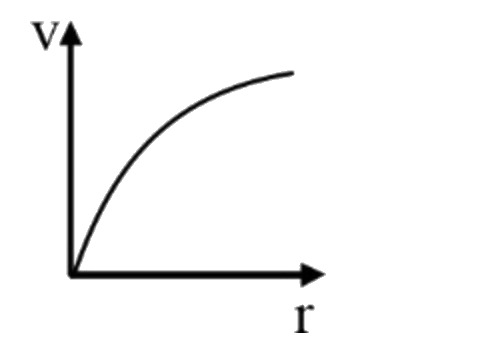 D
D
- Question 2 - Select One
A spherical liquid drop is placed on a horizontal plane . A small distrubance cause the volume of the drop to oscillate . The time period oscillation (T) of the liquid drop depends on radius (r) of the drop , density (ρ) and surface tension tension (S) of the liquid. Which amount the following will be be a possible expression for T (where k is a dimensionless constant)?
Ak√ρrSBk√ρ2rSCk√ρ2rSDk√ρr2S2 - Question 3 - Select One
The terminal velocity V of a spherical ball of lead of radius R falling through a viscous liquid varies with R such that
AVR= ConstantBVR= constantCV= constantDVR2= constant
If the time period (T)of vibration of a liquid drop depends on surface tension (S) , radius(r) of the drop , and density (ρ) of the liquid , then find the expression of T.
View SolutionWhy are falling liquid drops spherical?
View SolutionThe rain drops are in spherical shape due to
View SolutionThe shape of a rain drop is spherical due to -
View SolutionA sphere of radius R is gently dropped into liquid of viscosity η in a vertical uniform tube. It attains a terminal velocity v. Another sphere of radius 2 R when dropped into the same liquid, will attain its teriminal velocity.
View Solution

