For any real number x, let [x] denote the largest integer less than or equal to x. let f be a real valued function defined on the interval [−10,10] by
f(x)={x−[x]if[x]is odd1+[x]−xif[x]is even .
Then the value of ∫10−10f(x)cosπx is
20π2
40π2
−20π2
−40π2
To solve the given problem, we need to evaluate the integral:
I=∫10−10f(x)cos(πx)dx
where the function f(x) is defined as:
f(x)={x−(x)if (x) is odd1+(x)−xif (x) is even
Step 1: Analyze the function f(x)
The function f(x) depends on the integer part of x, denoted by (x). The behavior of f(x) will change based on whether (x) is odd or even.
- For x in the interval (n,n+1) where n is an integer:
- If n is even, then f(x)=1+n−x.
- If n is odd, then f(x)=x−n.
Step 2: Break the integral into intervals
We can break the integral from −10 to 10 into intervals of length 1:
I=9∑n=−10∫n+1nf(x)cos(πx)dx
Step 3: Evaluate each interval
We will evaluate the integral for each interval separately:
1. For n=−10 (even):
f(x)=1+(−10)−x=−9−xfor x∈(−10,−9)
∫−9−10(−9−x)cos(πx)dx
2. For n=−9 (odd):
f(x)=x−(−9)=x+9for x∈(−9,−8)
∫−8−9(x+9)cos(πx)dx
3. For n=−8 (even):
f(x)=1+(−8)−x=−7−xfor x∈(−8,−7)
∫−7−8(−7−x)cos(πx)dx
4. For n=−7 (odd):
f(x)=x+7for x∈(−7,−6)
∫−6−7(x+7)cos(πx)dx
5. Continue this process for all intervals up to n=9.
Step 4: Use symmetry
Notice that f(x) is periodic with period 2 and is an even function. The function cos(πx) is also even. Therefore, we can simplify our integral:
I=2∫100f(x)cos(πx)dx
Step 5: Evaluate from 0 to 2
Now we can evaluate:
∫20f(x)cos(πx)dx=∫10(1−x)cos(πx)dx+∫21(x−1)cos(πx)dx
Step 6: Compute the integrals
1. For ∫10(1−x)cos(πx)dx:
- Use integration by parts.
2. For ∫21(x−1)cos(πx)dx:
- Again, use integration by parts.
Step 7: Combine results
Combine the results of the integrals to find I.
Final Result
After evaluating all the integrals and combining them, we find:
I=40π2
- If n is even, then f(x)=1+n−x.
- If n is odd, then f(x)=x−n.
f(x)=1+(−10)−x=−9−xfor x∈(−10,−9)
∫−9−10(−9−x)cos(πx)dx
f(x)=x−(−9)=x+9for x∈(−9,−8)
∫−8−9(x+9)cos(πx)dx
f(x)=1+(−8)−x=−7−xfor x∈(−8,−7)
∫−7−8(−7−x)cos(πx)dx
f(x)=x+7for x∈(−7,−6)
∫−6−7(x+7)cos(πx)dx
- Use integration by parts.
- Again, use integration by parts.
Topper's Solved these Questions
Similar Questions
For any real number x,let[x] denote the largest integer less than or equal to x,Letf be a real-valued function defined on the interval [−10,10] be f(x)={x−[x],if[x]isodd1+[x]−x,if[x]iseven Then the value of π210∫10−1f(x)cosπxdxis__
View Solutionf(x)={x−[x],if[x]is odd1+[x]−x,if[x] is even
Then, the value of π210∫10−10f(x)cosπ×dx is
View Solution
Knowledge Check
For any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
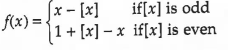 Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1
Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1For any real number x, let [x] denotes the largest integer less than or equal to x.Let f be a real valued function defined on the interval[-10,10] by
f(x)={(x−[x])<br>(1+[x]−x)}
Then, the value of π210∫10−10 f(x) cos π x dx isA2B4C0DNone of theseFor a real number x let [x] denote the largest number less than or equal to x. For x∈R let f (x)=[x] sinπx. Then
AIf is differentiable on R.Bf is symmetric about the line x=0C∫3−3f(x)dx=0DFor each real α, the equation f(x)−α=0 has infinitely many roots.
For any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
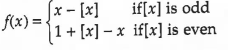 Then, the value of (π10)2(∫10−10f(x)cosπxdx is
Then, the value of (π10)2(∫10−10f(x)cosπxdx is
View SolutionFor any real number x, let [x] denote the largest integer less than or equal to x. If
∫100[√10xx+1]dx then the value of 9I is
View SolutionFor a real number x, let [x] denote the greatest integer less than or equal to x. Let f: R→ R be defined as f(x)=2x+[x]+sinxcosx then f is
View SolutionLet [x] denotes the greatest integer less than or equal to x and f(x)=[tan2x].Then
View SolutionLet [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
View Solution
