Linear mass density of rod varies as λ=λ0(1−(x2l2)). Find COM of rod.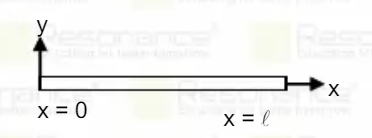 
a. l/2
b. l/4
c. 3l/8
d. 5l/12
Step by step video & image solution for Linear mass density of rod varies as lambda = lambda_0(1-(x^2/l^2)). Find COM of rod. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is λ=λ0x. The centre of mass of rod divides the length of the rod in the ratio:
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is λ such that λ=a+bx. Find the mass of the rod.
View Solution
Knowledge Check
- Question 1 - Select One
A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
AL/2B2L/3CL/4DL/5 - Question 2 - Select One
The adjacent figure shows a non-uniform metre stick AB having the linear mass density variation λ=λ0x , where λ0 is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is αA and in the second case it is αB then
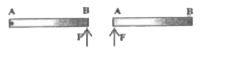AαA=αBBαA>αBCαA<αBDdata insufficient to determine
Linear charge densities of the two rods are given as λ1=−λ0xI2 and λ2=+λ0yl2. If the dipole moment of the system of rods is √mλ0ln, then find (m+n).
'(##CEN_KSR_PHY_JEE_C18_E01_009_Q02##)'View SolutionThe linear mass density lambda of a rod AB is given by λ=aplha+βxkgm taking O as origin. Find the location of the centre of mass from the end A?
View SolutionIf the linear density of a rod of length L varies as λ=A+Bx , find the position of its centre of mass .
View SolutionA rod of length 2m has uniform cross- section but linear mass density varies as λ=(1+x)kgm .It is placed as shown in figure.The moment of inertia of rod about an axis passing through O and perpendicular to rod is (x is in metre )
View SolutionThe linear mass density of a rod of length 2L varies with distance (x) from center as λ=λ0(1+xL) .The distance of COM from center is nL.Then n is
View SolutionThe linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
View Solution