Question

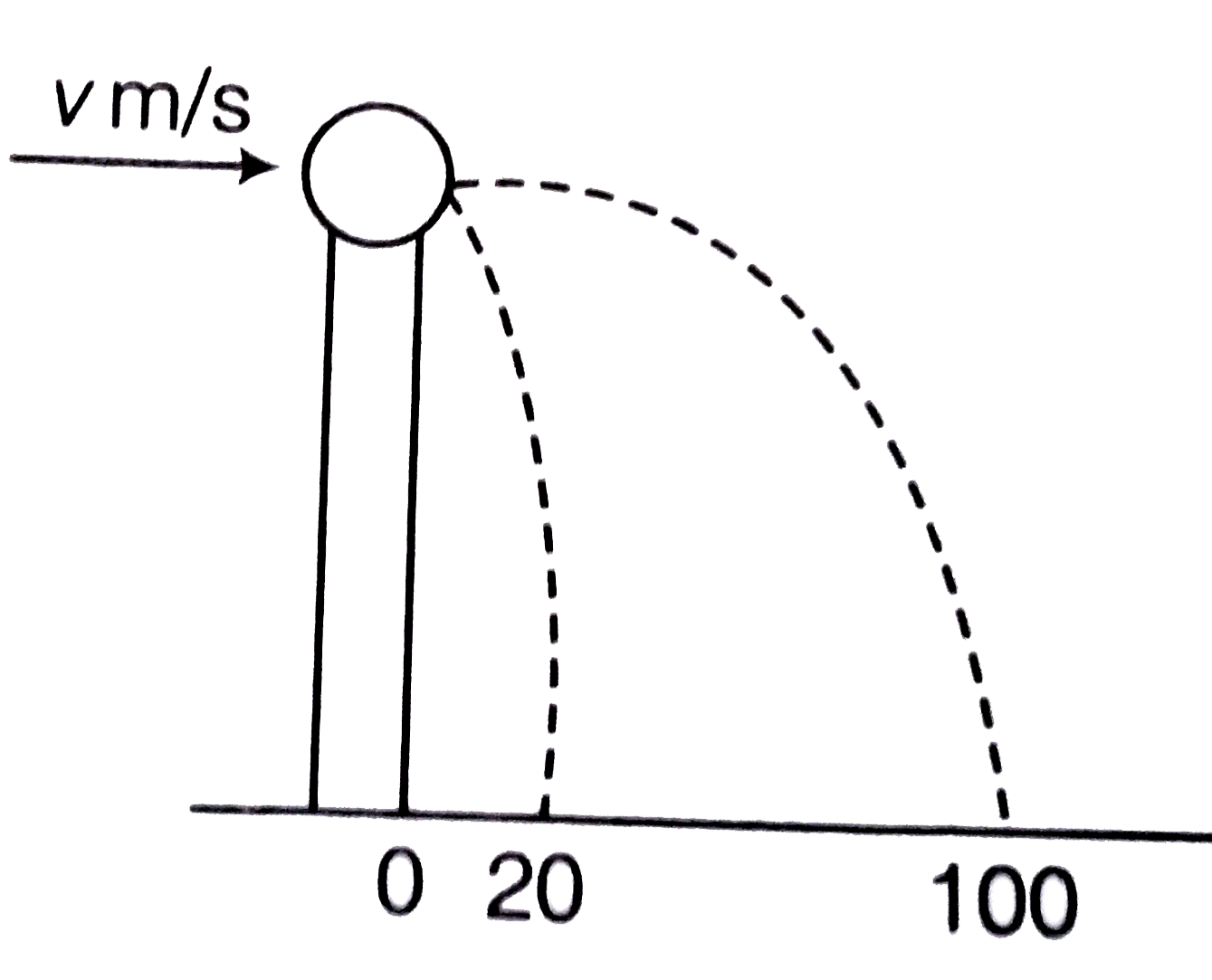
A ball of mass $200g$ rests on a vertical post of height $20m$.A bullet of mass $10g$,travelling in horizontal direction,hits the centre of the ball.After collision both travels independently.The ball hits the ground at a distance $30m$ and the bullet at a distance of $120m$ from the foot of the post.The value of initial velocity of the bullet will be (If $g=10\frac{m}{s^2}$ ) :

Options

A. `400m/s`
B. `360m/s`
C. `60m/s`
D. `120m/s`

Answer

B

Explanation

To solve the problem step by step, we will analyze the motion of the ball and the bullet separately and apply the principles of physics, particularly projectile motion and conservation of momentum.

Step 1: Determine the time of flight for the ball
The ball falls from a height of 20 m. We can use the equation of motion for free fall:

\( h = \frac{1}{2} g t^2 \)

Where:
- \( h = 20 \, \text{m} \) (height)
- \( g = 10 \, \text{m/s}^2 \) (acceleration due to gravity)
- \( t \) = time of flight

Rearranging the equation gives:

\( 20 = \frac{1}{2} \times 10 \times t^2 \)

\( 20 = 5t^2 \)

\( t^2 = \frac{20}{5} = 4 \)

\( t = \sqrt{4} = 2 \, \text{s} \)

Step 2: Calculate the horizontal velocity of the ball after the collision
The ball travels a horizontal distance of 30 m while falling. We can find its horizontal velocity \( V \) using the formula:

\( \text{Distance} = \text{Velocity} \times \text{Time} \)

Substituting the known values:

\( 30 = V \times 2 \)

Solving for \( V \):

\( V = \frac{30}{2} = 15 \, \text{m/s} \)

Step 3: Calculate the horizontal velocity of the bullet after the collision
The bullet travels a horizontal distance of 120 m in the same time of flight (2 seconds). We can find its horizontal velocity \( V' \):

\( 120 = V' \times 2 \)

Solving for \( V' \):

\( V' = \frac{120}{2} = 60 \, \text{m/s} \)

Step 4: Apply the conservation of momentum
Since the collision is elastic, we apply the conservation of momentum before and after the collision. Let \( u \) be the initial velocity of the bullet.

The total momentum before the collision is equal to the total momentum after the collision:

\( m_b \cdot u + m_{ball} \cdot 0 = m_b \cdot V' + m_{ball} \cdot V \)

Where:
- \( m_b = 10 \, \text{g} = 0.01 \, \text{kg} \) (mass of the bullet)
- \( m_{ball} = 200 \, \text{g} = 0.2 \, \text{kg} \) (mass of the ball)
- \( V' = 60 \, \text{m/s} \) (velocity of the bullet after collision)
- \( V = 15 \, \text{m/s} \) (velocity of the ball after collision)

Substituting the values:

\( 0.01u + 0 = 0.01 \cdot 60 + 0.2 \cdot 15 \)

Calculating the right side:

\( 0.01u = 0.6 + 3 \)

\( 0.01u = 3.6 \)

Solving for \( u \):

\( u = \frac{3.6}{0.01} = 360 \, \text{m/s} \)

Final Answer
The initial velocity of the bullet is \( 360 \, \text{m/s} \).

---