A square loop of area 23cm2 has a resistance of 10Ω.The loop is placed in uniform magnetic field of magnitude 40.0T.The plane of loop is perpendicular to the magnetic field.The work done in pulling the loop out of the magnetic field slowly and uniformly in 1.0 sec,will be
5×10−3J
1.0×10−4J
2.5×10−3J
1.0×10−3J
The correct Answer is:D
To solve the problem, we need to calculate the work done in pulling a square loop out of a magnetic field. Here’s a step-by-step breakdown of the solution:
Step 1: Convert Area to SI Units
The area of the loop is given as 23cm2. We need to convert this to square meters.
Area=23cm2=23×10−4m2=0.0023m2
Hint: Remember to convert square centimeters to square meters by multiplying by 10−4.
Step 2: Calculate the Side Length of the Square Loop
Since the area A of a square loop is given by A=L2, we can find the side length L.
L=√A=√0.0023≈0.04796m
Hint: To find the side length of a square from its area, take the square root of the area.
Step 3: Calculate the Induced EMF
The induced electromotive force (EMF) in the loop when it is pulled out of the magnetic field can be calculated using Faraday's law of electromagnetic induction. The formula for EMF (E) is:
E=B⋅L⋅v
Where:
- B=40T (magnetic field strength)
- L is the length of one side of the loop
- v is the velocity at which the loop is pulled out.
Given that the loop is pulled out uniformly in 1.0s, we can assume a constant velocity:
v=Lt=0.047961.0≈0.04796m/s
Now substituting the values into the EMF formula:
E=40⋅0.04796⋅0.04796≈0.0916V
Hint: The induced EMF can be calculated using the product of the magnetic field, the length of the loop, and the velocity.
Step 4: Calculate the Current in the Loop
Using Ohm's law, the current I flowing through the loop can be calculated as:
I=ER
Where R=10Ω:
I=0.091610≈0.00916A
Hint: Use Ohm's law to relate EMF, current, and resistance.
Step 5: Calculate the Force on the Loop
The force F acting on the loop due to the magnetic field can be calculated using the formula:
F=BIL
Substituting the values:
F=40⋅0.00916⋅0.04796≈0.0175N
Hint: The force on a current-carrying conductor in a magnetic field can be calculated using the product of the magnetic field, current, and length.
Step 6: Calculate the Work Done
The work done W in pulling the loop out of the magnetic field is given by:
W=F⋅d
Where d is the distance moved, which is equal to the length of the side of the loop L:
W=F⋅L=0.0175⋅0.04796≈0.000839J
Hint: Work done can be calculated as the product of force and the distance moved in the direction of the force.
Final Result
The work done in pulling the loop out of the magnetic field slowly and uniformly in 1.0s is approximately:
W≈0.000839J≈8.39×10−4J
The area of the loop is given as 23cm2. We need to convert this to square meters.
Since the area A of a square loop is given by A=L2, we can find the side length L.
The induced electromotive force (EMF) in the loop when it is pulled out of the magnetic field can be calculated using Faraday's law of electromagnetic induction. The formula for EMF (E) is:
- B=40T (magnetic field strength)
- L is the length of one side of the loop
- v is the velocity at which the loop is pulled out.
Using Ohm's law, the current I flowing through the loop can be calculated as:
The force F acting on the loop due to the magnetic field can be calculated using the formula:
The work done W in pulling the loop out of the magnetic field is given by:
The work done in pulling the loop out of the magnetic field slowly and uniformly in 1.0s is approximately:
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Figure show a square loop of side 0.5m and resistance 10Ω. The magnetic field has a magnitude B=1.0T. The work done in pulling the loop out of the field slowly and uniformly in 2.0s is
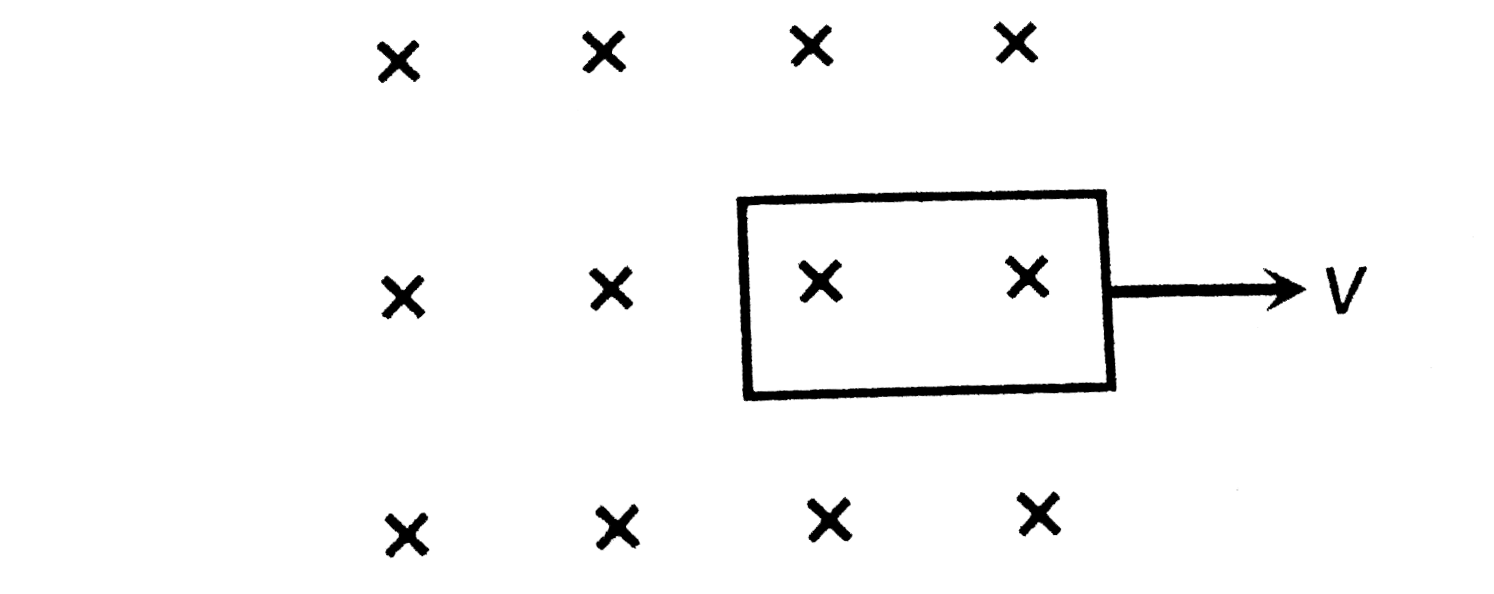 A3.125×10−3JB6.25×10−4JC1.25×10−2JD5.0×10−4J
A3.125×10−3JB6.25×10−4JC1.25×10−2JD5.0×10−4J - Question 2 - Select One
Figure shows loop of 200 turns and side a=3m and resistance of one coil R=1000Ω. The work done in pulling the loop out of the field, slowly and uniformly in 1.0 s is
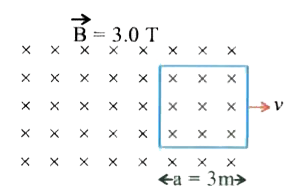 A130 JB125 JC146 JDNone
A130 JB125 JC146 JDNone - Question 3 - Select One
A wire loop that encloses an area of 20cm2 has a resistance of 10Ω The loop is placed in a magnetic field of 2.4 T with its plane perpendicular to the field . The loop is suddenly removed from the field. How much charge flows past a given point in the wire ?
A12×10−4CB3.6×10−1CC4.8×10−4CD2.4×10−3C
A metallic loop is placed in a nonuiform magnetic field. Will an emf be induced in the loop?
View SolutionA circular loop of radius 0⋅2m carrying a current of 1A is placed in a uniform magnetic field of 0⋅5T. The magnetic field is perpendicular to the plane of the loop. What is the force experienced by the loop?
View SolutionA wire loop is rotated in a uniform magnetic field about an axis perpendicular to the field. The direction of the current induced in the loop reverses in each
View SolutionA conducting circular loop is placed in a uniform magnetic field 0.04T with its plane perpendicular to the magnetic field. The radius of the loop starts shrinking at 2mm/sec . The induced emf in the loop when the radius is 2cm is
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in newton in both the cases a and b. The radius of the loop is 1.0 m
 View Solution
View Solution

