A point charge 2×10−2 is moved form P to S in a uniform electric field of 30NC−1 directed along positive x -axis.If coordinates of P and S are (1,2,0)m and (0,0,0)m respectively,the work done by electric field will be
600mJ
−1200mJ
−600mJ
1200mJ
The correct Answer is:C
To find the work done by the electric field when moving a point charge from point P to point S, we can follow these steps:
Step 1: Identify the given values
- Charge, Q=2×10−2C
- Electric field, E=30N/C
- Initial position, P(1,2,0)m
- Final position, S(0,0,0)m
Step 2: Calculate the displacement vector
The displacement vector →d from point P to point S can be calculated as:
→d=→S−→P=(0,0,0)−(1,2,0)=(−1,−2,0)m
Step 3: Calculate the work done by the electric field
The work done W by the electric field when moving a charge is given by the formula:
W=Q⋅→E⋅→d
Where →E is the electric field vector. Since the electric field is directed along the positive x-axis, we can represent it as:
→E=(30,0,0)N/C
Step 4: Calculate the dot product →E⋅→d
Now, we calculate the dot product:
→E⋅→d=(30,0,0)⋅(−1,−2,0)=30×(−1)+0×(−2)+0×0=−30N m/C
Step 5: Substitute into the work formula
Now substituting the values into the work formula:
W=Q⋅(→E⋅→d)=(2×10−2)⋅(−30)=−0.6J
Step 6: Convert to millijoules
To express this in millijoules:
W=−0.6J=−600mJ
Final Answer
The work done by the electric field is:
W=−600mJ
---
- Charge, Q=2×10−2C
- Electric field, E=30N/C
- Initial position, P(1,2,0)m
- Final position, S(0,0,0)m
The displacement vector →d from point P to point S can be calculated as:
→d=→S−→P=(0,0,0)−(1,2,0)=(−1,−2,0)m
The work done W by the electric field when moving a charge is given by the formula:
W=Q⋅→E⋅→d
Where →E is the electric field vector. Since the electric field is directed along the positive x-axis, we can represent it as:
→E=(30,0,0)N/C
Now, we calculate the dot product:
→E⋅→d=(30,0,0)⋅(−1,−2,0)=30×(−1)+0×(−2)+0×0=−30N m/C
Now substituting the values into the work formula:
W=Q⋅(→E⋅→d)=(2×10−2)⋅(−30)=−0.6J
To express this in millijoules:
W=−0.6J=−600mJ
The work done by the electric field is:
W=−600mJ
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A positively charge particle moving along x-axis with a certain velocity enters a uniform electric field directed along positively y-axis. Its
AVertical velocity changes but horizontal velocity remains constantBHorizontal velocity changes but vertical velocity remiand constantCBoth vertical and horizontal velocities changeDNeither vertical nor horizontal velocity changes. - Question 2 - Select One
A uniform electric field E=2×103NC−1 is acting along the positive x-axis. The flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane is
A20NC−1m2B30NC−1m2C10NC−1m2D40NC−1m2 - Question 3 - Select One
A uniform electric field E=2×103NC−1 is acting along the positive x-axis. The flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane is
A20NC−1m2B30NC−1m2C10NC−1m2D40NC−1m2
A point charge q moves from point P to pont S along the path PQRS (fig.) in a uniform electric field E pointing parallel to the poistive direction of the X-axis. The coordinates of the points P, Q, R and S are(a, b, O), (2a, O, O)(a, -b,O––) and (O, O, O) respectively. The work done by the field in the above process is given by the expresison............
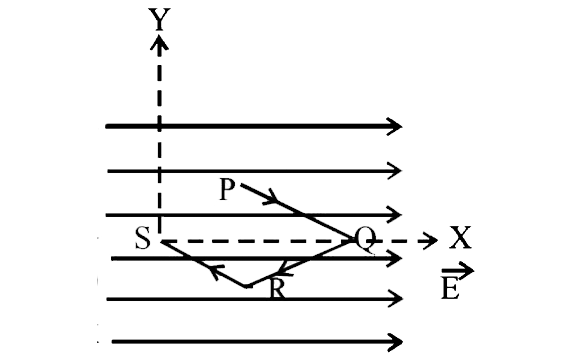 View Solution
View SolutionA region contains a uniform electric field ¯¯¯E=(10ˆi+30ˆj)Vm−1 A and B are two points in the field at (1,2,0)m and (2,1,3)m respectively.The work done when a charge 0.8C moves from A and B in a parabolic path is?
View SolutionTwo point charges of, 1 μC and -1 μC are kept at (-2 m, 0) and (2 m, 0) respectively. Calculate the electric field at point (0, 5 m).
View SolutionA uniform electric field of 30NC−1 exists along the X-axis calculate the potential difference VB−VA between the points A (4m,2m) and B(10m,5m).
View SolutionA uniform electric field of 200 V / m is directed at 45∘ with x -axis as shown in figure. The co-ordinates of point P and point Q are (1,0) and ( 0,2) . Find the potential difference , VP−VQ ( in volts) .
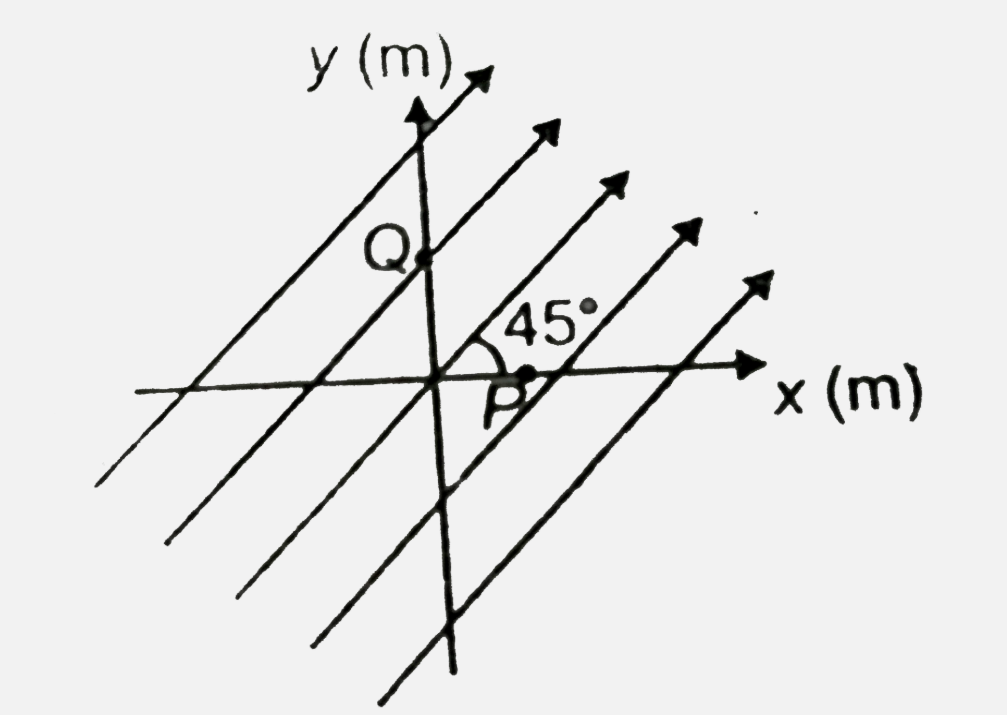 View Solution
View Solution

