The electric current in a circular coil of four turns produces a magnetic induction 32T at its centre.The coil is unwound and is rewound into a circular coil of single turn,the magnetic induction at the centre of the coil by the same current will be
8T
2T
4T
16T
The correct Answer is:B
To solve the problem, we need to understand how the magnetic induction (magnetic field) at the center of a coil changes when the number of turns in the coil changes.
1. Understanding the Magnetic Induction Formula:
The magnetic induction B at the center of a circular coil can be expressed using the formula:
B=μ0nI2R
where:
- B is the magnetic induction,
- μ0 is the permeability of free space,
- n is the number of turns,
- I is the current,
- R is the radius of the coil.
2. Given Values:
- For the initial coil with 4 turns, the magnetic induction B1=32T.
- Thus, we can write:
B1=μ0⋅4⋅I2R1
3. Rewinding the Coil:
- When the coil is unwound and rewound into a single turn, the number of turns n becomes 1.
- The radius of the new coil R2 will be different, but we need to find the new magnetic induction B2.
4. Relating the Two Coils:
- The total length of wire remains the same when the coil is unwound and rewound.
- The length of wire used in the first coil is L1=2πR1⋅4 (for 4 turns).
- The length of wire used in the second coil is L2=2πR2⋅1 (for 1 turn).
- Setting these equal gives:
2πR1⋅4=2πR2⋅1⟹R2=4R1
5. Calculating the New Magnetic Induction:
- Now substituting R2 back into the formula for B2:
B2=μ0⋅1⋅I2R2=μ0⋅I2(4R1)=μ0⋅I8R1
6. Relating B1 and B2:
- We know from our first equation:
B1=μ0⋅4⋅I2R1⟹B1=2μ0⋅IR1
- Thus, we can express B2 in terms of B1:
B2=B14=324=8T
Final Answer:
The magnetic induction at the center of the single-turn coil is 8T.
The magnetic induction B at the center of a circular coil can be expressed using the formula:
B=μ0nI2R
where:
- B is the magnetic induction,
- μ0 is the permeability of free space,
- n is the number of turns,
- I is the current,
- R is the radius of the coil.
- For the initial coil with 4 turns, the magnetic induction B1=32T.
- Thus, we can write:
B1=μ0⋅4⋅I2R1
- When the coil is unwound and rewound into a single turn, the number of turns n becomes 1.
- The radius of the new coil R2 will be different, but we need to find the new magnetic induction B2.
- The total length of wire remains the same when the coil is unwound and rewound.
- The length of wire used in the first coil is L1=2πR1⋅4 (for 4 turns).
- The length of wire used in the second coil is L2=2πR2⋅1 (for 1 turn).
- Setting these equal gives:
2πR1⋅4=2πR2⋅1⟹R2=4R1
- Now substituting R2 back into the formula for B2:
B2=μ0⋅1⋅I2R2=μ0⋅I2(4R1)=μ0⋅I8R1
- We know from our first equation:
B1=μ0⋅4⋅I2R1⟹B1=2μ0⋅IR1
- Thus, we can express B2 in terms of B1:
B2=B14=324=8T
The magnetic induction at the center of the single-turn coil is 8T.
Topper's Solved these Questions
Similar Questions
When a long wire carrying a steady current is best into a circular coil of one turn, the magnetic induction at its centre is B. When the same wire carrying the same current is bent into a circular coil of one turn, the magnetic induction at its centre is B. when the same wire carrying the same current is bent to form a circular coil of a turns of a smaller radius, the magnetic induction at the centre will be
View SolutionA current passing through a circular coil of two turns produces a magnetic field B as its centr. The coil is then rewound so as to have four turns and the same current is passed through it. The magnetic field at its centre now is
View Solution
Knowledge Check
- Question 1 - Select One
The electric current in a circular coil of two turns produced a magnetic induction of 0.2 T at its centre. The coil is unwound and then rewound into a circular coil of four turns. If same current flows in the coil, the magnetic induction at the centre of the coil now is
A0.2TB0.4TC0.6TD0.8T - Question 2 - Select One
A current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
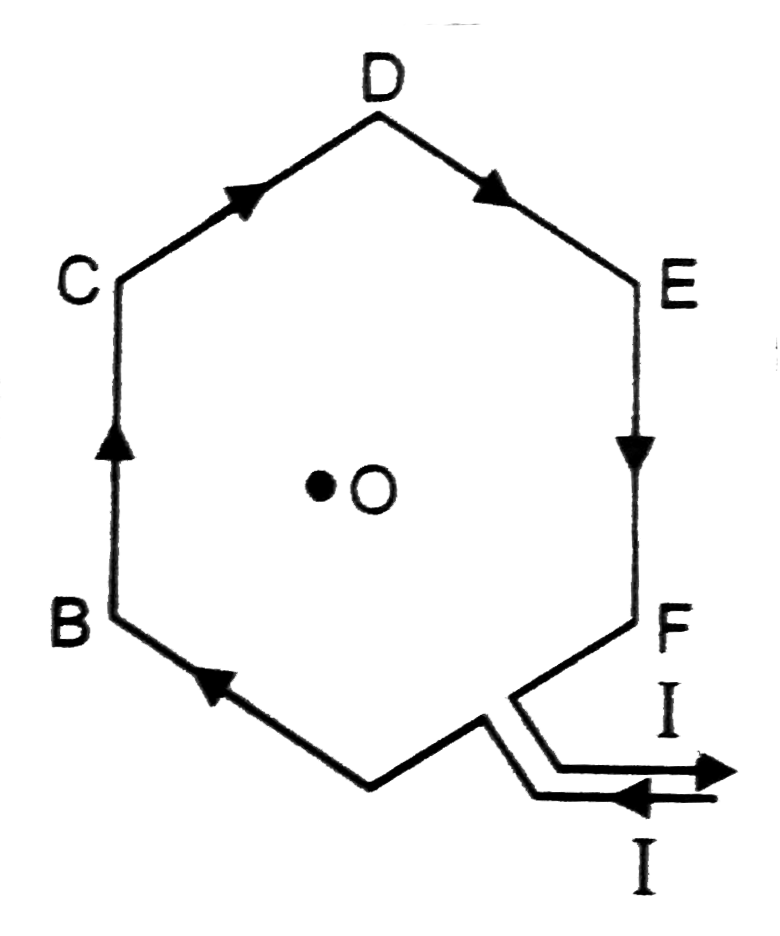 Aμ0I3√3πaB√3μ0IπaC3√3μ0IπaDμ0I√3πa
Aμ0I3√3πaB√3μ0IπaC3√3μ0IπaDμ0I√3πa - Question 3 - Select One
A current I is flowing in an octagonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
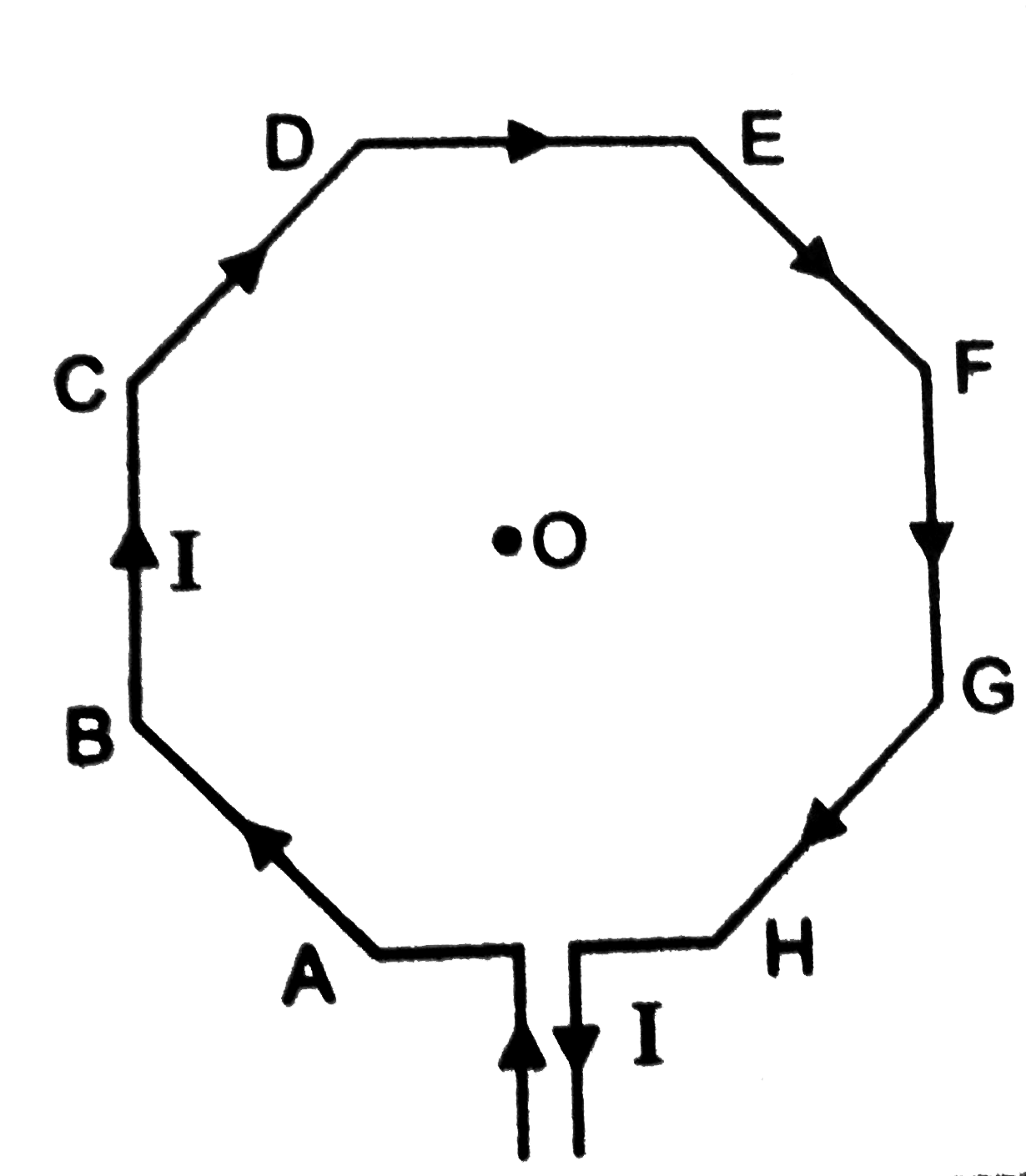 A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πa
A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πa
When a certain length of wire is turned into one circular loop, the magnetic induction at the centre of coil due to some current flowing is B1 If the same wire is turned into three loops to make a circular coil, the magnetic induction at the center of this coil for the same current will be
View SolutionA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. It is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
 View Solution
View SolutionA circular coil of radius 'r' having 'n' turns carries a current 'I'. The magnetic induction at the center of the coil is 'B'. Now the coil is unwound and rewound with half the original radius. If the magnetic induction at the center of the coil is to be the same, the current that should be passed through the coil is
View Solution

