The product [ab−ba][a−bba] is equal to
[a2+b200a2+b2]
[(a+b)20(a+b)20]
[a2+b20a2+b20]
[a00b]
To solve the problem of finding the product of the two matrices ((a,b),(−b,a)) and ((a,−b),(b,a)), we will follow the steps of matrix multiplication.
Step 1: Identify the matrices
Let
A=(ab−ba)
and
B=(a−bba)
Step 2: Set up the multiplication
The product AB will be calculated as follows:
AB=(ab−ba)(a−bba)
Step 3: Calculate the elements of the product matrix
The product of two matrices is calculated by taking the dot product of rows from the first matrix with columns from the second matrix.
1. First row, first column:
(a⋅a)+(b⋅b)=a2+b2
2. First row, second column:
(a⋅−b)+(b⋅a)=−ab+ab=0
3. Second row, first column:
(−b⋅a)+(a⋅b)=−ab+ab=0
4. Second row, second column:
(−b⋅−b)+(a⋅a)=b2+a2
Step 4: Write the resulting matrix
Combining all these results, we get:
AB=(a2+b200a2+b2)
Final Result
Thus, the product of the two matrices is:
AB=(a2+b2)I
where I is the identity matrix.
Let
A=(ab−ba)
and
B=(a−bba)
The product AB will be calculated as follows:
AB=(ab−ba)(a−bba)
The product of two matrices is calculated by taking the dot product of rows from the first matrix with columns from the second matrix.
(a⋅a)+(b⋅b)=a2+b2
(a⋅−b)+(b⋅a)=−ab+ab=0
(−b⋅a)+(a⋅b)=−ab+ab=0
(−b⋅−b)+(a⋅a)=b2+a2
Combining all these results, we get:
AB=(a2+b200a2+b2)
Thus, the product of the two matrices is:
AB=(a2+b2)I
where I is the identity matrix.
Topper's Solved these Questions
Similar Questions
Knowledge Check
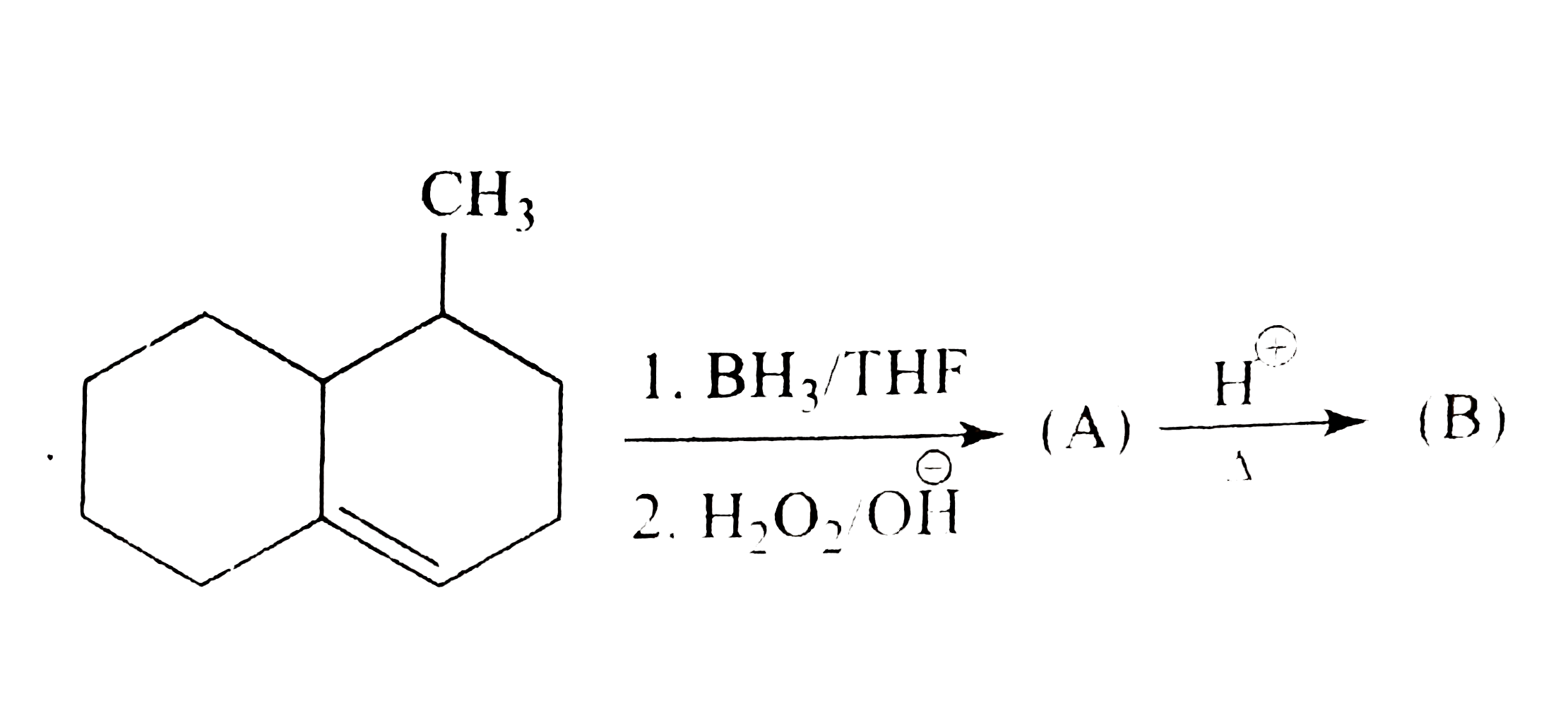 The product (B) is :A
The product (B) is :A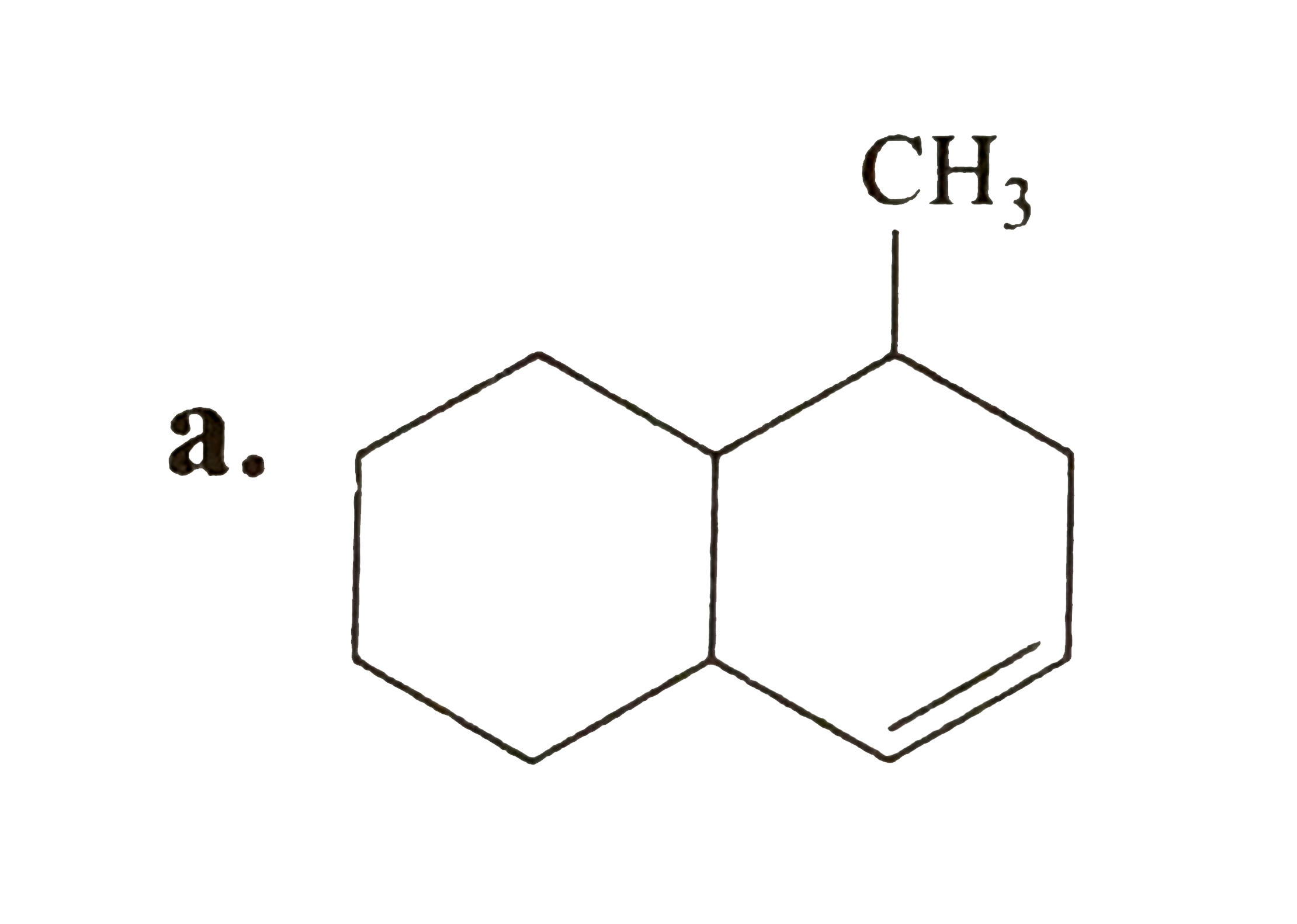 B
B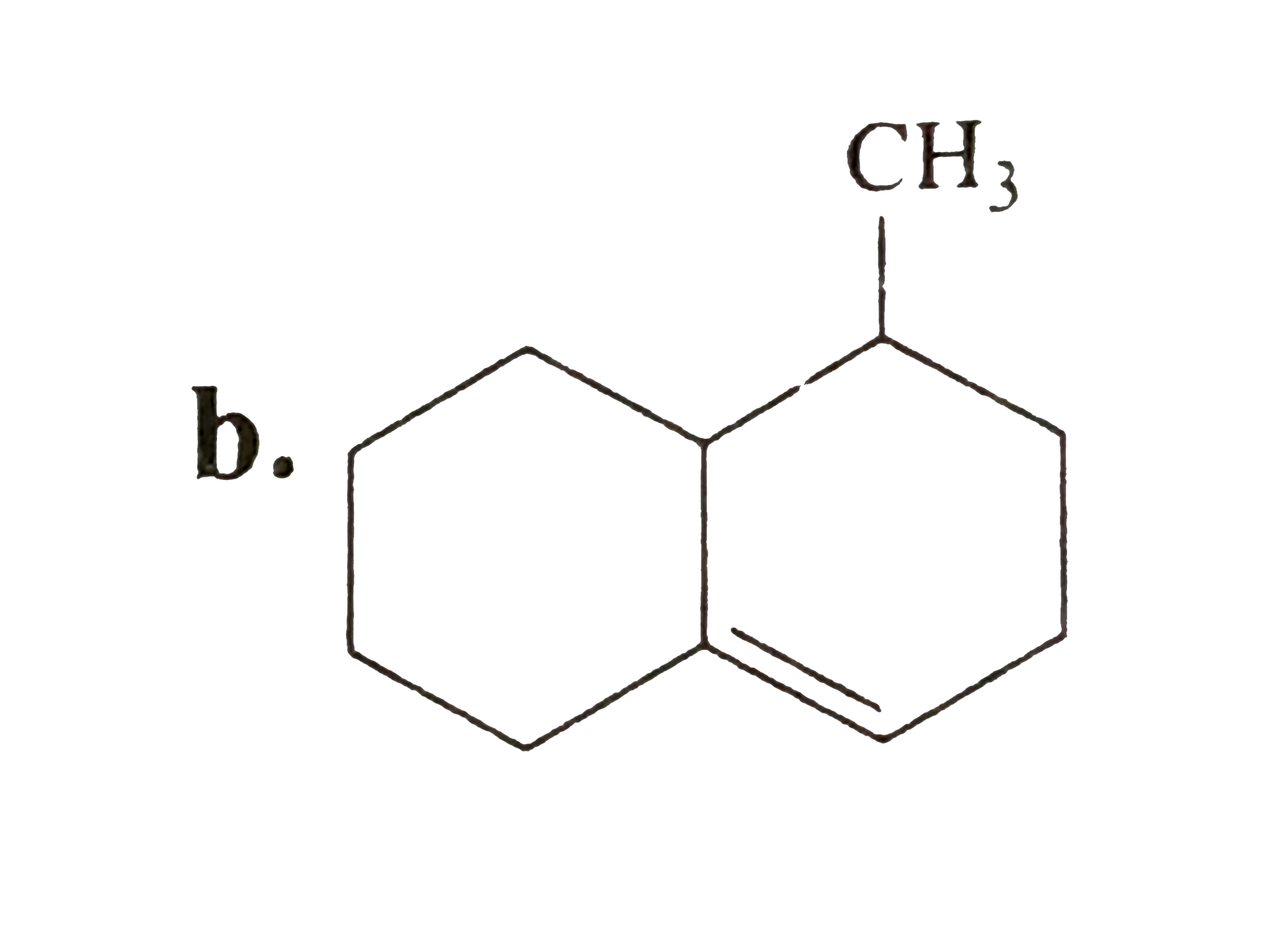 C
C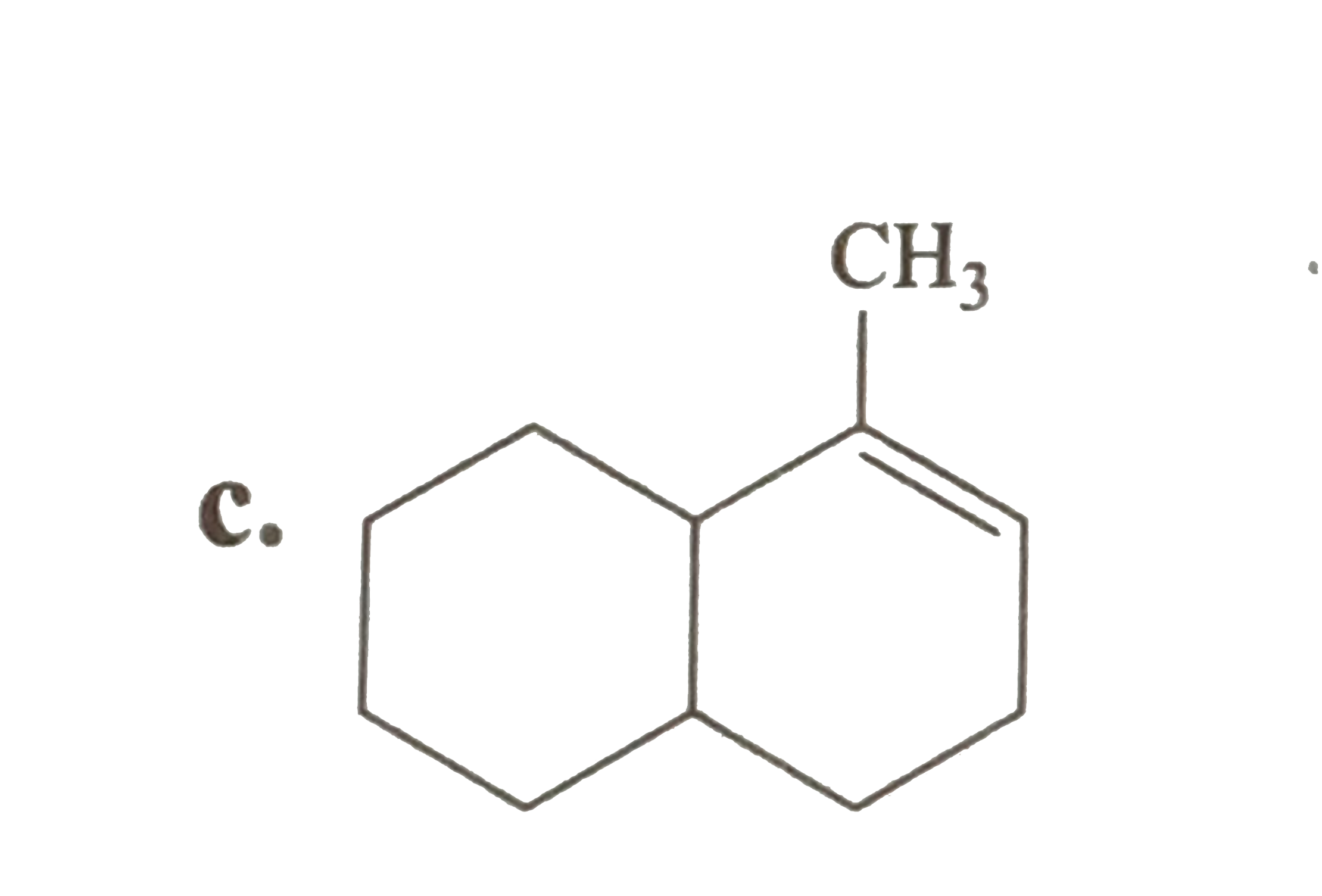 DAll
DAll(a+b)×(a−b) is equal to
Aa2−b2B2(a×b)C2(b×a)Dnone of these∣∣ ∣∣abcbcacab∣∣ ∣∣ is equal to
Aa+b+c+abcBa2+b2+c2+ab+bc+caC3abc−a2−b3−c3Da3+b3+c3−3abc
If tanx=ba then √a+ba−b+√a−ba+b is equal to
View SolutionIf tanα=ba a>b>0 and if 0<α<π4 then √a+ba−b−√a−ba+b is equal to
View Solution∣∣ ∣∣a+babaa+ccbcb+c∣∣ ∣∣ is equal to
View Solution∣∣ ∣∣a+babaa+ccbcb+c∣∣ ∣∣ is equal to
View SolutionIf the vectors a, b and c are coplanar, then ∣∣ ∣∣abca.aa.ba.cb.ab.bb.c∣∣ ∣∣ is equal to
View Solution
