Which of the following points satisfies both the inequalities and ?
To determine which of the given points satisfies both inequalities 2x+y≤10 and x+2y≥8, we will evaluate each point one by one.
1. Identify the inequalities:
- First inequality: 2x+y≤10 (let's call this Inequality 1)
- Second inequality: x+2y≥8 (let's call this Inequality 2)
2. Evaluate the first point (-2, 4):
- For Inequality 1:
2(−2)+4=−4+4=0(which is ≤10)
This satisfies Inequality 1.
- For Inequality 2:
−2+2(4)=−2+8=6(which is not ≥8)
This does not satisfy Inequality 2.
- Conclusion: Point (-2, 4) does not satisfy both inequalities.
3. Evaluate the second point (3, 2):
- For Inequality 1:
2(3)+2=6+2=8(which is ≤10)
This satisfies Inequality 1.
- For Inequality 2:
3+2(2)=3+4=7(which is not ≥8)
This does not satisfy Inequality 2.
- Conclusion: Point (3, 2) does not satisfy both inequalities.
4. Evaluate the third point (-5, 6):
- For Inequality 1:
2(−5)+6=−10+6=−4(which is ≤10)
This satisfies Inequality 1.
- For Inequality 2:
−5+2(6)=−5+12=7(which is not ≥8)
This does not satisfy Inequality 2.
- Conclusion: Point (-5, 6) does not satisfy both inequalities.
5. Evaluate the fourth point (4, 2):
- For Inequality 1:
2(4)+2=8+2=10(which is ≤10)
This satisfies Inequality 1.
- For Inequality 2:
4+2(2)=4+4=8(which is ≥8)
This satisfies Inequality 2.
- Conclusion: Point (4, 2) satisfies both inequalities.
Final Answer:
The point that satisfies both inequalities is (4, 2).
- First inequality: 2x+y≤10 (let's call this Inequality 1)
- Second inequality: x+2y≥8 (let's call this Inequality 2)
- For Inequality 1:
2(−2)+4=−4+4=0(which is ≤10)
This satisfies Inequality 1.
- For Inequality 2:
−2+2(4)=−2+8=6(which is not ≥8)
This does not satisfy Inequality 2.
- Conclusion: Point (-2, 4) does not satisfy both inequalities.
- For Inequality 1:
2(3)+2=6+2=8(which is ≤10)
This satisfies Inequality 1.
- For Inequality 2:
3+2(2)=3+4=7(which is not ≥8)
This does not satisfy Inequality 2.
- Conclusion: Point (3, 2) does not satisfy both inequalities.
- For Inequality 1:
2(−5)+6=−10+6=−4(which is ≤10)
This satisfies Inequality 1.
- For Inequality 2:
−5+2(6)=−5+12=7(which is not ≥8)
This does not satisfy Inequality 2.
- Conclusion: Point (-5, 6) does not satisfy both inequalities.
- For Inequality 1:
2(4)+2=8+2=10(which is ≤10)
This satisfies Inequality 1.
- For Inequality 2:
4+2(2)=4+4=8(which is ≥8)
This satisfies Inequality 2.
- Conclusion: Point (4, 2) satisfies both inequalities.
The point that satisfies both inequalities is (4, 2).
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which one of the following values of x,y satisfies the equations 2x+3y≤6:x≥0,y≥0?
Ax = 0, y = 3Bx = 1, y = 2Cx = 1, y = 1Dx = 4, y = 0The solution set of the linear inequalities 2x+2y≥10 and x+2y≥10
A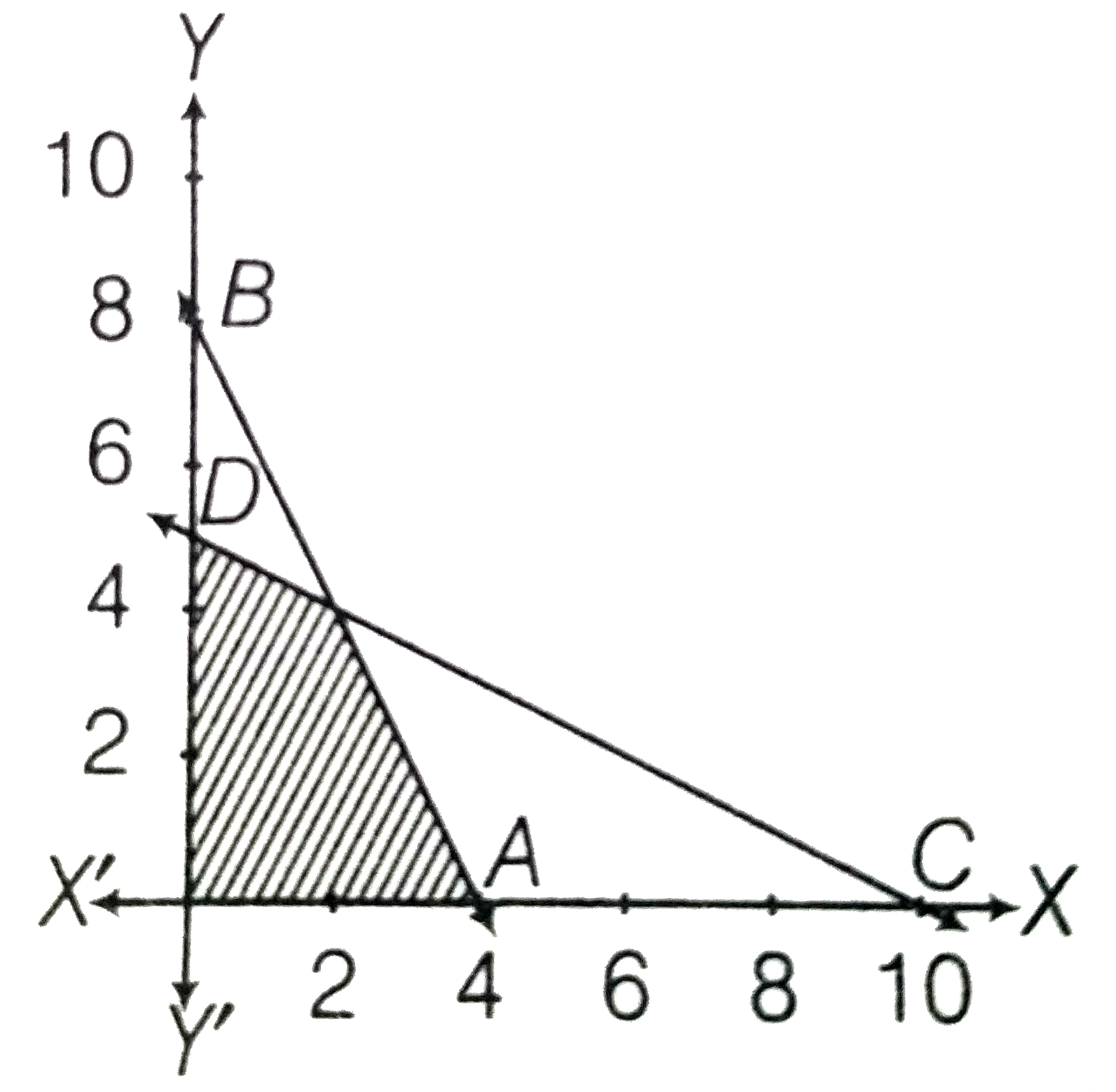 B
B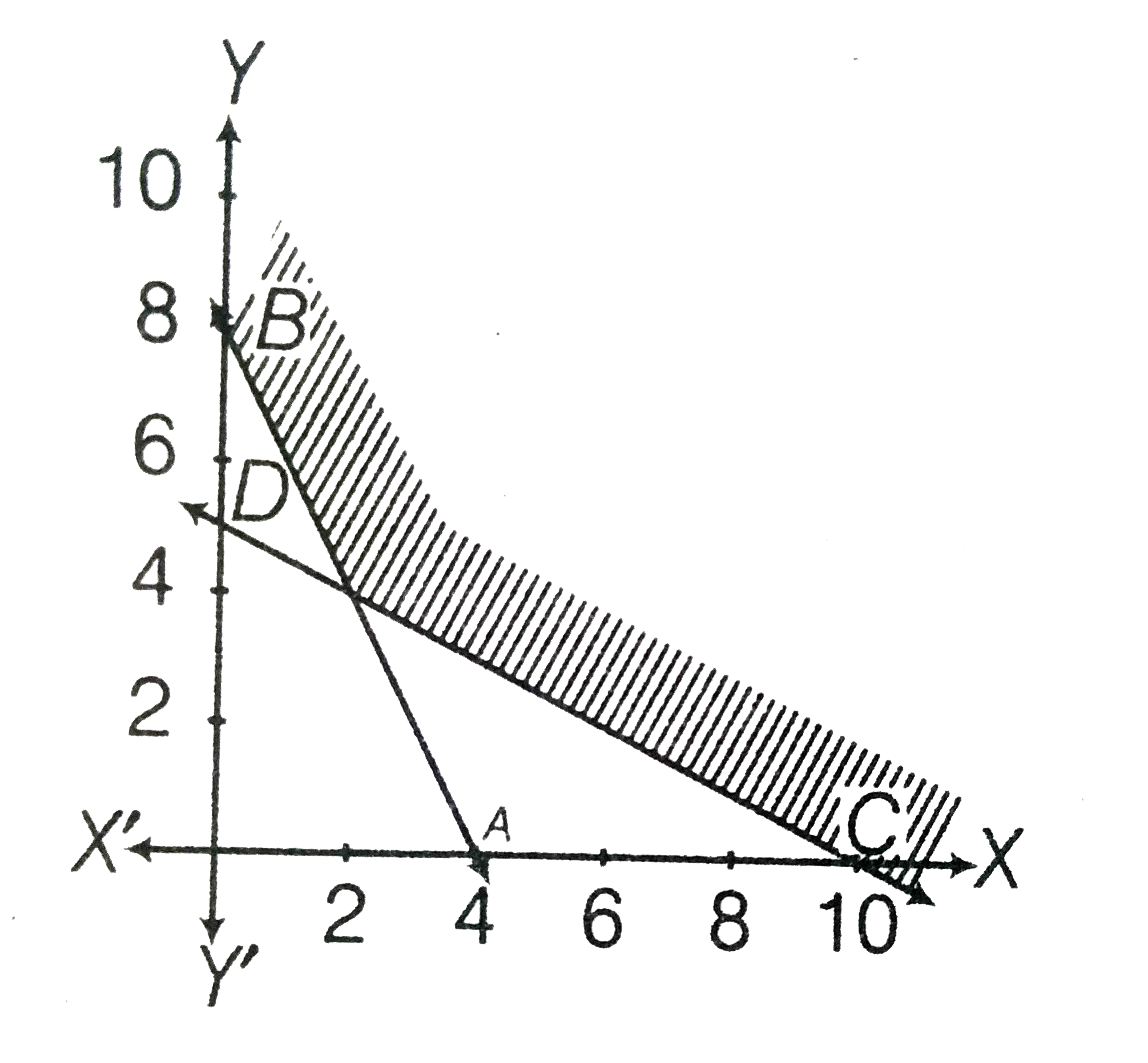 C
C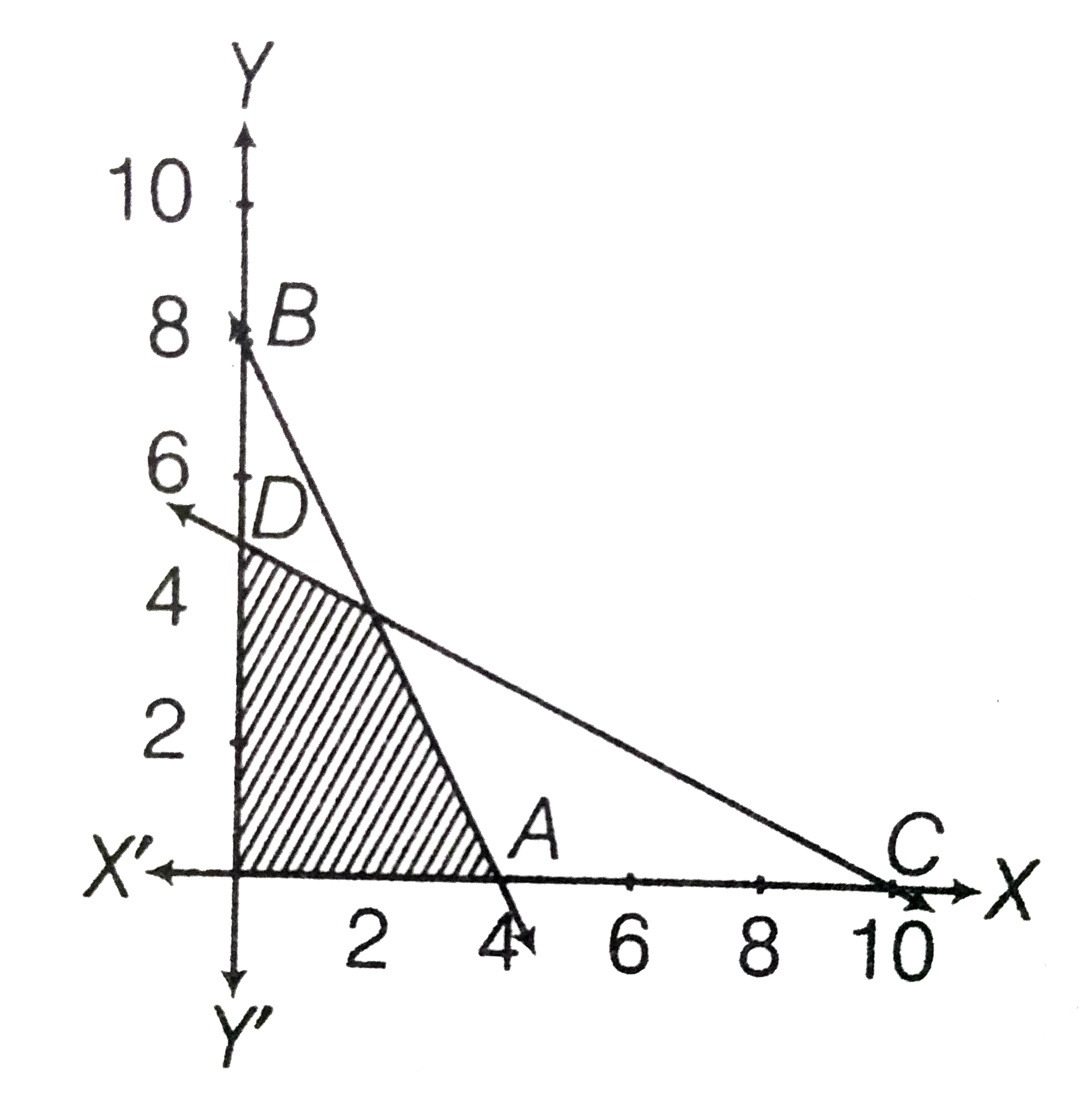 DNone of these
DNone of theseWhich one of the following values of x, y satisfies the in equation 2x+3y≥6,x≥0,y≥0?
Ax=0,y=3Bx=1,y=2Cx=1,y=1Dx=4,y=0
2x+y≥8,x+2y≥10
View SolutionThe solution set of the linear inequalities 2x+y≥8 and x+2y≥10 is
View SolutionThe solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
View SolutionThe values of x which satisfy both the inequations x2−1≤0andx2−x−2≥0 lie in
View Solutionthe corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
View Solution
