The solution set of the linear inequalities and is
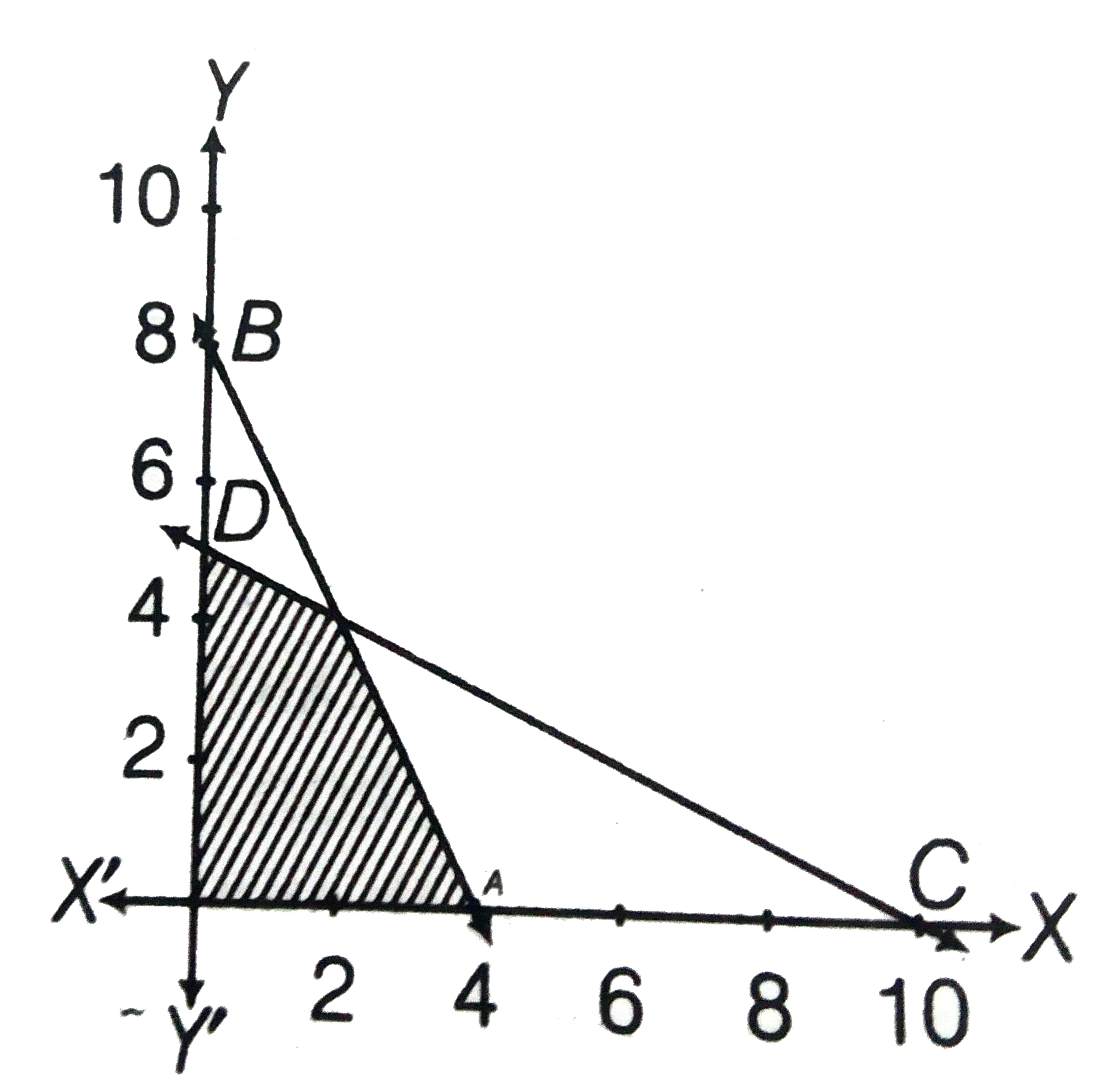
None of these
The correct Answer is:C
To solve the linear inequalities 2x+y≥8 and x+2y≥10, we will follow these steps:
Step 1: Convert inequalities to equations
We start by converting the inequalities into equations to find the boundary lines.
1. For the first inequality 2x+y=8.
2. For the second inequality x+2y=10.
Step 2: Find intercepts for the first equation
To graph the line 2x+y=8, we can find the x-intercept and y-intercept.
- X-intercept: Set y=0:
2x+0=8⟹x=4
So, the x-intercept is (4,0).
- Y-intercept: Set x=0:
2(0)+y=8⟹y=8
So, the y-intercept is (0,8).
Step 3: Find intercepts for the second equation
Next, we find the intercepts for the line x+2y=10.
- X-intercept: Set y=0:
x+2(0)=10⟹x=10
So, the x-intercept is (10,0).
- Y-intercept: Set x=0:
0+2y=10⟹y=5
So, the y-intercept is (0,5).
Step 4: Graph the lines
Now we will graph the two lines using the intercepts we found:
1. Draw the line through the points (4,0) and (0,8) for the equation 2x+y=8.
2. Draw the line through the points (10,0) and (0,5) for the equation x+2y=10.
Step 5: Determine the feasible region
To find the solution set for the inequalities, we need to identify which side of the lines satisfies the inequalities.
1. For 2x+y≥8:
- Test the origin (0,0):
2(0)+0≥8⟹0≥8(False)
- Since the origin does not satisfy the inequality, the feasible region is above the line 2x+y=8.
2. For x+2y≥10:
- Test the origin (0,0):
0+2(0)≥10⟹0≥10(False)
- Since the origin does not satisfy this inequality either, the feasible region is above the line x+2y=10.
Step 6: Identify the intersection of the regions
The solution set is the region that is above both lines. This region is unbounded and extends infinitely in the direction where both inequalities are satisfied.
Final Solution
The solution set of the linear inequalities 2x+y≥8 and x+2y≥10 is the region above both lines in the coordinate plane.
---
We start by converting the inequalities into equations to find the boundary lines.
2. For the second inequality x+2y=10.
To graph the line 2x+y=8, we can find the x-intercept and y-intercept.
2x+0=8⟹x=4
So, the x-intercept is (4,0).
2(0)+y=8⟹y=8
So, the y-intercept is (0,8).
Next, we find the intercepts for the line x+2y=10.
x+2(0)=10⟹x=10
So, the x-intercept is (10,0).
0+2y=10⟹y=5
So, the y-intercept is (0,5).
Now we will graph the two lines using the intercepts we found:
2. Draw the line through the points (10,0) and (0,5) for the equation x+2y=10.
To find the solution set for the inequalities, we need to identify which side of the lines satisfies the inequalities.
- Test the origin (0,0):
2(0)+0≥8⟹0≥8(False)
- Since the origin does not satisfy the inequality, the feasible region is above the line 2x+y=8.
- Test the origin (0,0):
0+2(0)≥10⟹0≥10(False)
- Since the origin does not satisfy this inequality either, the feasible region is above the line x+2y=10.
The solution set is the region that is above both lines. This region is unbounded and extends infinitely in the direction where both inequalities are satisfied.
The solution set of the linear inequalities 2x+y≥8 and x+2y≥10 is the region above both lines in the coordinate plane.
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )15videos
Linear Programming
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )30videos
Linear Programming
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner3videos
LINE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER22videos
MATHEMATICAL LOGIC
Similar Questions
Knowledge Check
- Question 1 - Select One
The solution set of the linear inequalities 2x+2y≥10 and x+2y≥10
A B
B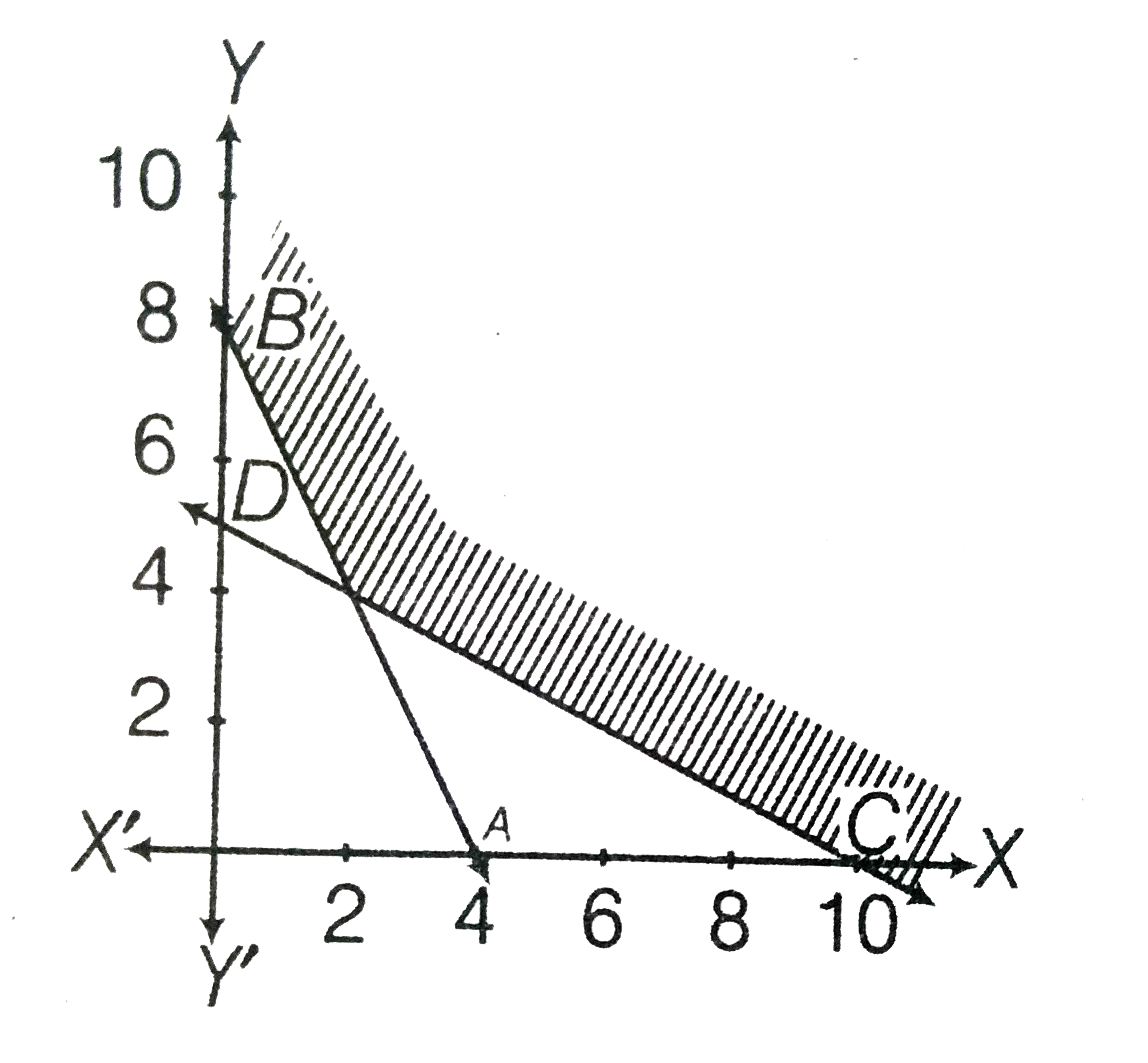 C
C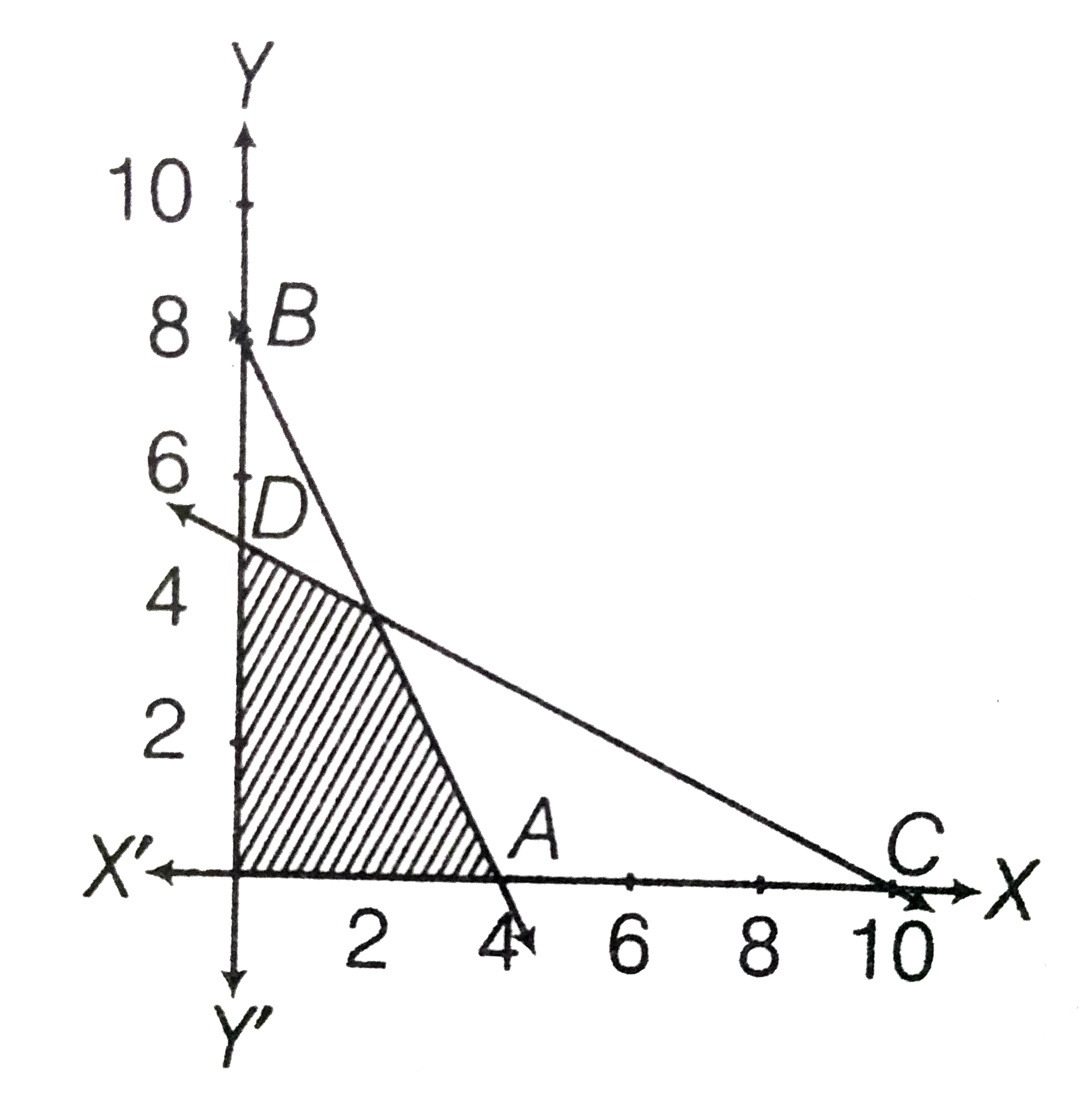 DNone of these
DNone of these - Question 2 - Select One
The solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
A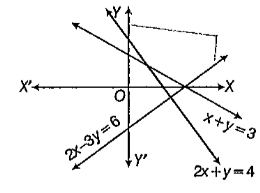 B
B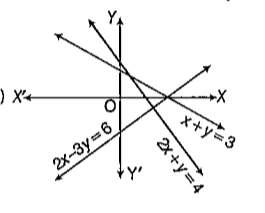 C
C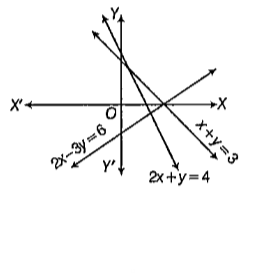 D
D
- Question 3 - Select One
The graphical solution of linear inequalities x+y≥5 and x−y≤3,
A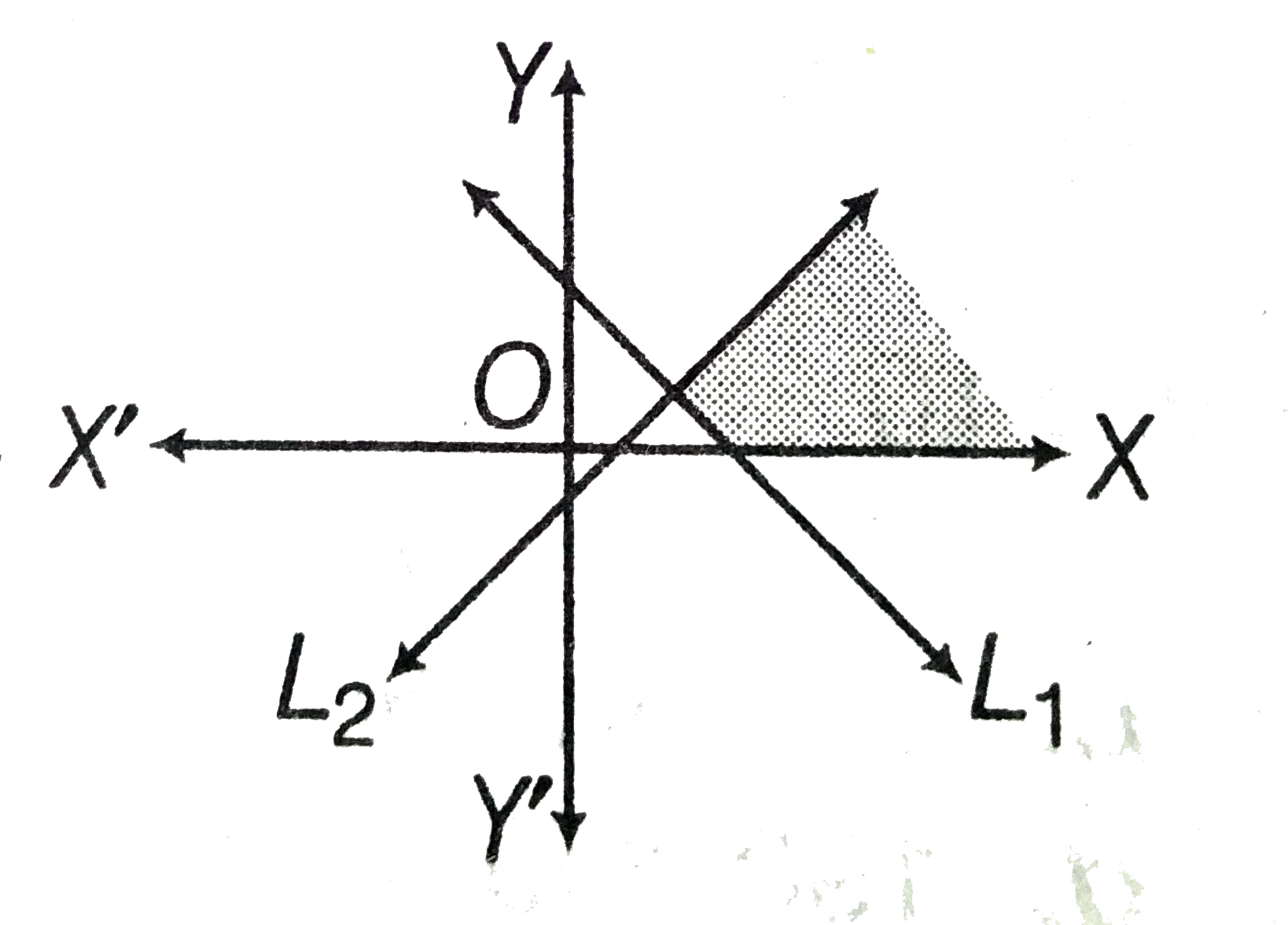 B
B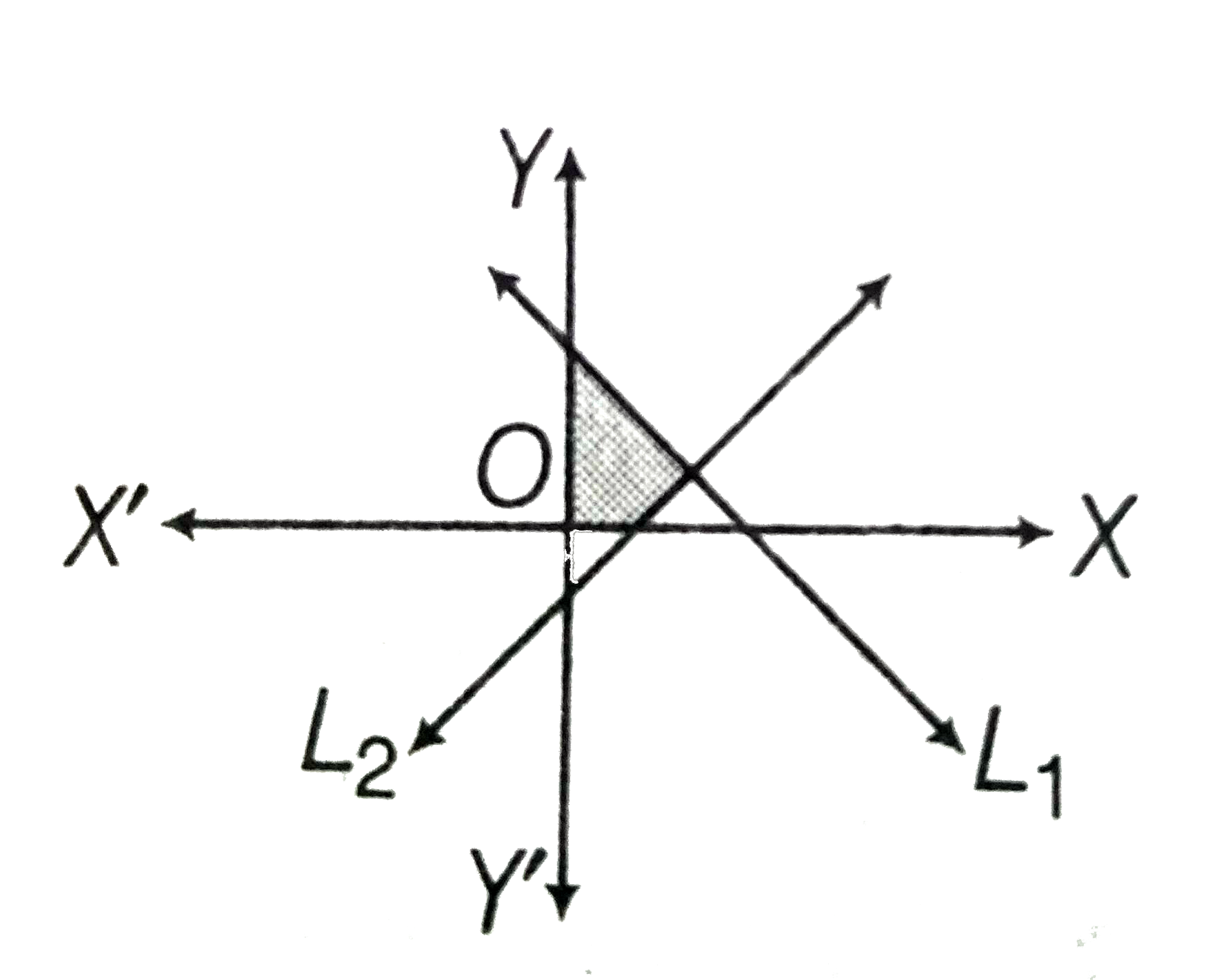 C
C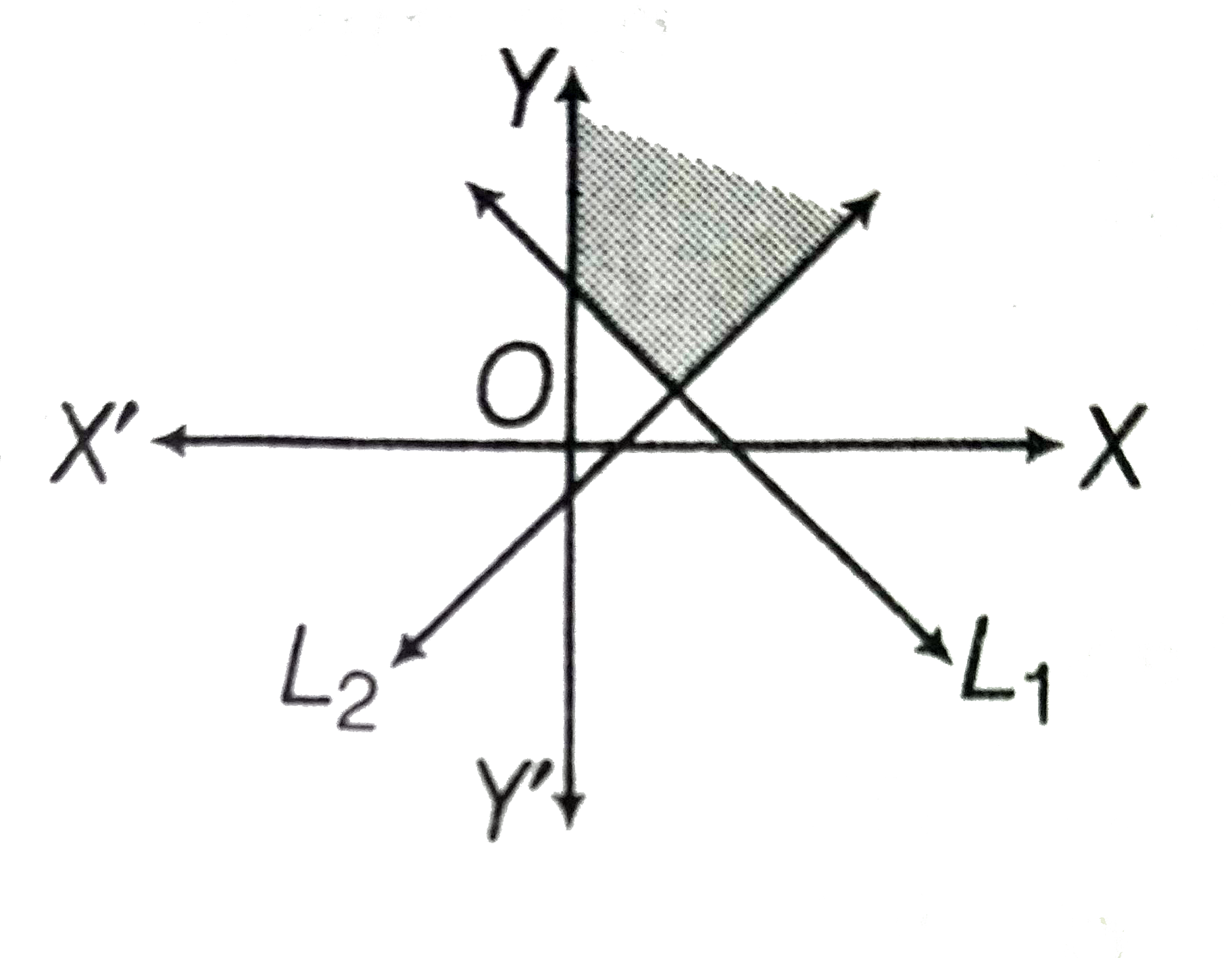 D
D
The shaded region representing the solution set of the system of inequalities x−2y≤3,3x+4y≥12,x≥0,y≥1 in the following figure is
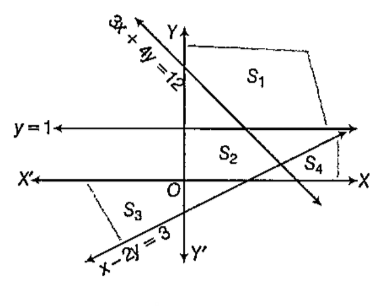 View Solution
View SolutionThe solution of the system of inequalities x≥0,y≥0,5x+2y≥10,6x+5y≤30 is a polygonal region with the vertices _________
View SolutionThe solution set of the inequation
3|x|+2≥1, isView SolutionThe region represented by the solution set of the system of inequalities x−y≤1,x+2y≤8,2x+y≥2,0,y≥0is
View SolutionThe graphical solution of the inequalities x+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0 is
View Solution

