A particle is moving with constant speed in a circular path. When the particle turns by an angle 90∘, the ratio of instantaneous velocity to its average velocity is π:√2 . The value of x will be
2
5
1
7
The correct Answer is:A
To solve the problem, we need to analyze the motion of a particle moving in a circular path and understand the relationship between instantaneous velocity and average velocity when the particle turns by an angle of 90∘.
1. Understanding the Motion:
- The particle moves in a circular path with a constant speed. When it turns by an angle of 90∘, it covers a quarter of the circular path.
2. Defining Variables:
- Let the radius of the circular path be r.
- The distance covered by the particle when it turns by 90∘ is the length of the arc, which can be calculated as:
Arc length=r⋅θ=r⋅π2(since θ=90∘=π2 radians)
3. Calculating Average Velocity:
- The average velocity (Vavg) is defined as the total displacement divided by the total time taken.
- The displacement when the particle moves 90∘ is the straight-line distance from the starting point to the endpoint, which forms the hypotenuse of a right triangle:
Displacement=r√2
- If t is the time taken to move through the 90∘, then the average velocity is:
Vavg=Displacementt=r√2t
4. Calculating Instantaneous Velocity:
- The instantaneous velocity (Vinst) at any point in circular motion is directed tangentially to the path. Since the particle is moving with constant speed, the magnitude of the instantaneous velocity is the same as the speed of the particle.
- Let this speed be v. Thus, we have:
Vinst=v
5. Finding the Ratio:
- According to the problem, the ratio of instantaneous velocity to average velocity is given as:
VinstVavg=vr√2t=vtr√2
- We know from the problem statement that this ratio equals π√2:
vtr√2=π√2
6. Solving for x:
- Rearranging the equation gives:
vt=rπ
- Since v=2πrT (where T is the time period for a full circular motion), we can substitute v into the equation:
2πrTt=rπ
- Dividing both sides by r (assuming r≠0):
2πtT=π
- Simplifying gives:
2t=T⇒t=T2
7. Final Calculation:
- The value of x in the ratio vVavg=πx√2 is found by equating:
x=2
Thus, the value of x is 2.
- The particle moves in a circular path with a constant speed. When it turns by an angle of 90∘, it covers a quarter of the circular path.
- Let the radius of the circular path be r.
- The distance covered by the particle when it turns by 90∘ is the length of the arc, which can be calculated as:
Arc length=r⋅θ=r⋅π2(since θ=90∘=π2 radians)
- The average velocity (Vavg) is defined as the total displacement divided by the total time taken.
- The displacement when the particle moves 90∘ is the straight-line distance from the starting point to the endpoint, which forms the hypotenuse of a right triangle:
Displacement=r√2
- If t is the time taken to move through the 90∘, then the average velocity is:
Vavg=Displacementt=r√2t
- The instantaneous velocity (Vinst) at any point in circular motion is directed tangentially to the path. Since the particle is moving with constant speed, the magnitude of the instantaneous velocity is the same as the speed of the particle.
- Let this speed be v. Thus, we have:
Vinst=v
- According to the problem, the ratio of instantaneous velocity to average velocity is given as:
VinstVavg=vr√2t=vtr√2
- We know from the problem statement that this ratio equals π√2:
vtr√2=π√2
- Rearranging the equation gives:
vt=rπ
- Since v=2πrT (where T is the time period for a full circular motion), we can substitute v into the equation:
2πrTt=rπ
- Dividing both sides by r (assuming r≠0):
2πtT=π
- Simplifying gives:
2t=T⇒t=T2
- The value of x in the ratio vVavg=πx√2 is found by equating:
x=2
Topper's Solved these Questions
Similar Questions
Knowledge Check
When particle revolves with uniform speed on a circular path
Ano force acts on itBno acceleration acts on itCno work is done by itDits velocity is constantA particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
A2vBv(vπ)Cv2Dv2πThe ratio of instantaneous velocity and the average speed of the particle performing S.H.M. is
A2πB2πCπ2Dπ2√1−x2A2
A particle is moving with constant speed v on a circular path of 'r' radius when it has moved by angle 60∘, Find
(i) Displacement of particle
(ii) Average velocity
(iii) Average acceleration
View SolutionAngular momentum of a single particle moving with constant speed along circular path :
View SolutionA particle is moving with a constant speed in a circular orbit. Find the change in its velocity when it completes half the revolution.
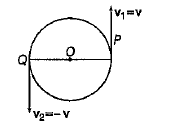
View SolutionA particle moves with uniform speed in a circular path the angle between instantaneous velocity and acceleration is
View SolutionA particle is moving on a circular path with constant speed, then its acceleration will be
View Solution
