Two planets A and B have thermal conductivities 84Wm−1K−1 and 126Wm−1K−1 respectively They have same surface area and same thickness. They are placed in contact along their surface .If the temperatures of the outer surface of A and B are kept at 100∘C and 0∘C respectively , then the temperature of the surface of contect in steady state is ___^@C
To solve the problem, we need to find the temperature at the interface of two planets A and B in steady state, given their thermal conductivities and the temperatures of their outer surfaces.
1. Identify Given Values:
- Thermal conductivity of planet A, KA=84Wm−1K−1
- Thermal conductivity of planet B, KB=126Wm−1K−1
- Temperature of the outer surface of A, TA=100∘C
- Temperature of the outer surface of B, TB=0∘C
2. Set Up the Heat Transfer Equation:
In steady state, the heat transfer through both planets must be equal. The heat transfer H through a material is given by the formula:
H=K⋅A⋅(T1−T2)L
where K is the thermal conductivity, A is the surface area, T1 and T2 are the temperatures on either side, and L is the thickness.
Since both planets have the same surface area A and thickness L, we can simplify our equation:
KA⋅(TA−T)=KB⋅(T−TB)
where T is the temperature at the interface.
3. Substitute Known Values:
Substitute the known values into the equation:
84⋅(100−T)=126⋅(T−0)
4. Expand and Rearrange the Equation:
Expanding both sides gives:
8400−84T=126T
Rearranging the equation to isolate T:
8400=126T+84T
8400=210T
5. Solve for T:
Dividing both sides by 210:
T=8400210=40∘C
Final Answer:
The temperature of the surface of contact in steady state is 40∘C.
- Thermal conductivity of planet A, KA=84Wm−1K−1
- Thermal conductivity of planet B, KB=126Wm−1K−1
- Temperature of the outer surface of A, TA=100∘C
- Temperature of the outer surface of B, TB=0∘C
In steady state, the heat transfer through both planets must be equal. The heat transfer H through a material is given by the formula:
H=K⋅A⋅(T1−T2)L
where K is the thermal conductivity, A is the surface area, T1 and T2 are the temperatures on either side, and L is the thickness.
KA⋅(TA−T)=KB⋅(T−TB)
where T is the temperature at the interface.
Substitute the known values into the equation:
84⋅(100−T)=126⋅(T−0)
Expanding both sides gives:
8400−84T=126T
Rearranging the equation to isolate T:
8400=126T+84T
8400=210T
Dividing both sides by 210:
T=8400210=40∘C
The temperature of the surface of contact in steady state is 40∘C.
Topper's Solved these Questions
Similar Questions
A wall consists of two layer, one of thickness 3 cm and other of 6 cm. the thermal conductivities of the materials of these layers are K and 3K respectively. The temperature of the outer surfaces of the two layers are −5∘C and 20∘C respectively. determine the temperature of the surface of contact of the two layers in the steady state.
View SolutionTwo walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
View Solution
Knowledge Check
Three rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
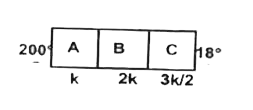 A156∘CB148∘CC116∘CD74∘C
A156∘CB148∘CC116∘CD74∘CTwo bars of thermal conductivities K and 3K and lengths 1cm and 2cm respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite bar is 0∘C and K2/l respectively (see figure), then the temperature ϕ of the interface is
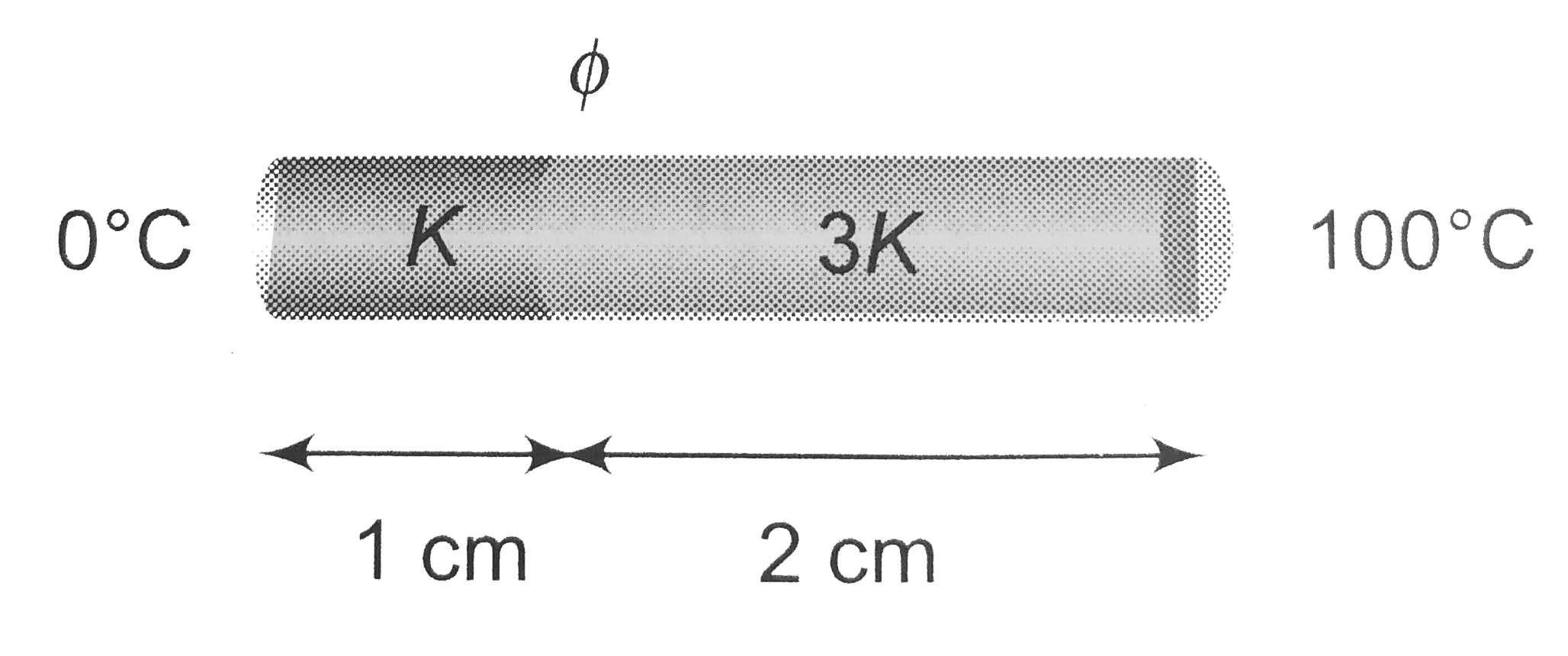 A50∘CB1003.∘CC60∘CD2003.∘C
A50∘CB1003.∘CC60∘CD2003.∘CIn a steady state of thermal conduction, temperature of the ends A and B of a 20 cm long rod are 100∘C and 0∘C respectively. What will be the temperature of the rod at a point at a distance of 6 cm from the end A of the rod
A−30∘CB70∘CC5∘CDNone of the above
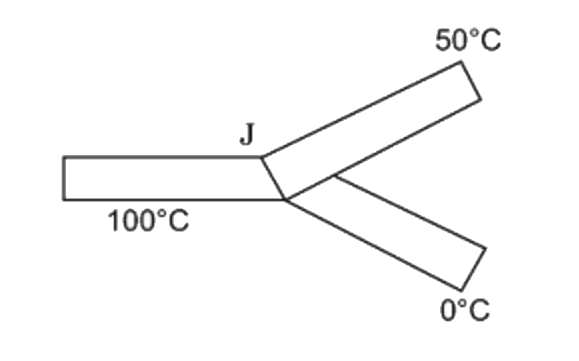
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below

Then , the temperature of the junction in steady - state is
View SolutionThree rods of same dimensions have thermal conductivities 3K, 2k and K, with their ends at 100∘C,50∘Cand0∘C respectively . They re arranged as shown in the diagram . The temperature of the junction J in steady -state is
View SolutionTwo materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
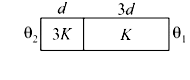
View SolutionIn the figure ABC is a conducting rod whose lateral surfaces are insulated. The length of the section AB is one-half of that of BC, and the respective thermal conductivities of the two sections are as given in the figure. If the ends A and C are maintained at 0∘C and 70∘C respectively, the temperature of junction B in the steady state is

View SolutionA solid cube and a sphere are made of the same material and both have the same surface area. If both are at the temperature of 300 K then initial
View Solution
