Two identical cells each of emf 1.5 V are connected in series across a 10Ω resistance.An ideal voltmeter connected across 10Ω resistance reads 1.5 V.The internal resistance of each cell is ________Ω.
To solve the problem, we need to determine the internal resistance of each cell when two identical cells are connected in series across a 10 Ω resistor, and the voltmeter reads 1.5 V across the resistor.
1. Understand the Circuit Configuration:
- We have two identical cells, each with an emf (E) of 1.5 V.
- The total emf when connected in series is Etotal=E1+E2=1.5V+1.5V=3V.
- The external resistance (R) is 10 Ω.
2. Identify the Variables:
- Let the internal resistance of each cell be r.
- Therefore, the total internal resistance of the two cells in series is 2r.
3. Apply Ohm's Law:
- The total voltage in the circuit is equal to the sum of the voltage across the external resistor and the voltage drop across the internal resistances.
- According to the problem, the voltmeter reads 1.5 V across the 10 Ω resistor.
4. Set Up the Equation:
- The voltage across the external resistor can be expressed as:
VR=I⋅R
- The total voltage provided by the cells can be expressed as:
Etotal=I⋅(R+2r)
- Since VR=1.5V and R=10Ω, we can express the current I as:
I=VRR=1.510=0.15A
5. Substituting Values:
- From the total voltage equation:
3=I⋅(10+2r)
- Substituting I=0.15:
3=0.15⋅(10+2r)
6. Solving for r:
- Rearranging gives:
3=1.5+0.3r
- Subtracting 1.5 from both sides:
1.5=0.3r
- Dividing by 0.3:
r=1.50.3=5Ω
7. Conclusion:
- The internal resistance of each cell is r=5Ω.
Final Answer:
The internal resistance of each cell is 5 Ω.
- We have two identical cells, each with an emf (E) of 1.5 V.
- The total emf when connected in series is Etotal=E1+E2=1.5V+1.5V=3V.
- The external resistance (R) is 10 Ω.
- Let the internal resistance of each cell be r.
- Therefore, the total internal resistance of the two cells in series is 2r.
- The total voltage in the circuit is equal to the sum of the voltage across the external resistor and the voltage drop across the internal resistances.
- According to the problem, the voltmeter reads 1.5 V across the 10 Ω resistor.
- The voltage across the external resistor can be expressed as:
VR=I⋅R
- The total voltage provided by the cells can be expressed as:
Etotal=I⋅(R+2r)
- Since VR=1.5V and R=10Ω, we can express the current I as:
I=VRR=1.510=0.15A
- From the total voltage equation:
3=I⋅(10+2r)
- Substituting I=0.15:
3=0.15⋅(10+2r)
- Rearranging gives:
3=1.5+0.3r
- Subtracting 1.5 from both sides:
1.5=0.3r
- Dividing by 0.3:
r=1.50.3=5Ω
- The internal resistance of each cell is r=5Ω.
The internal resistance of each cell is 5 Ω.
Topper's Solved these Questions
Similar Questions
In the given circuit, an ideal voltmeter connected across the 10Ω resistance reads 2V. The internal resistance r, of each cell is:
 View Solution
View SolutionIn the circuit shown, reading of the voltmeter connected across 400Ω resistance is 60 V. If it is connected across 300Ω resistance then reading in volt will be
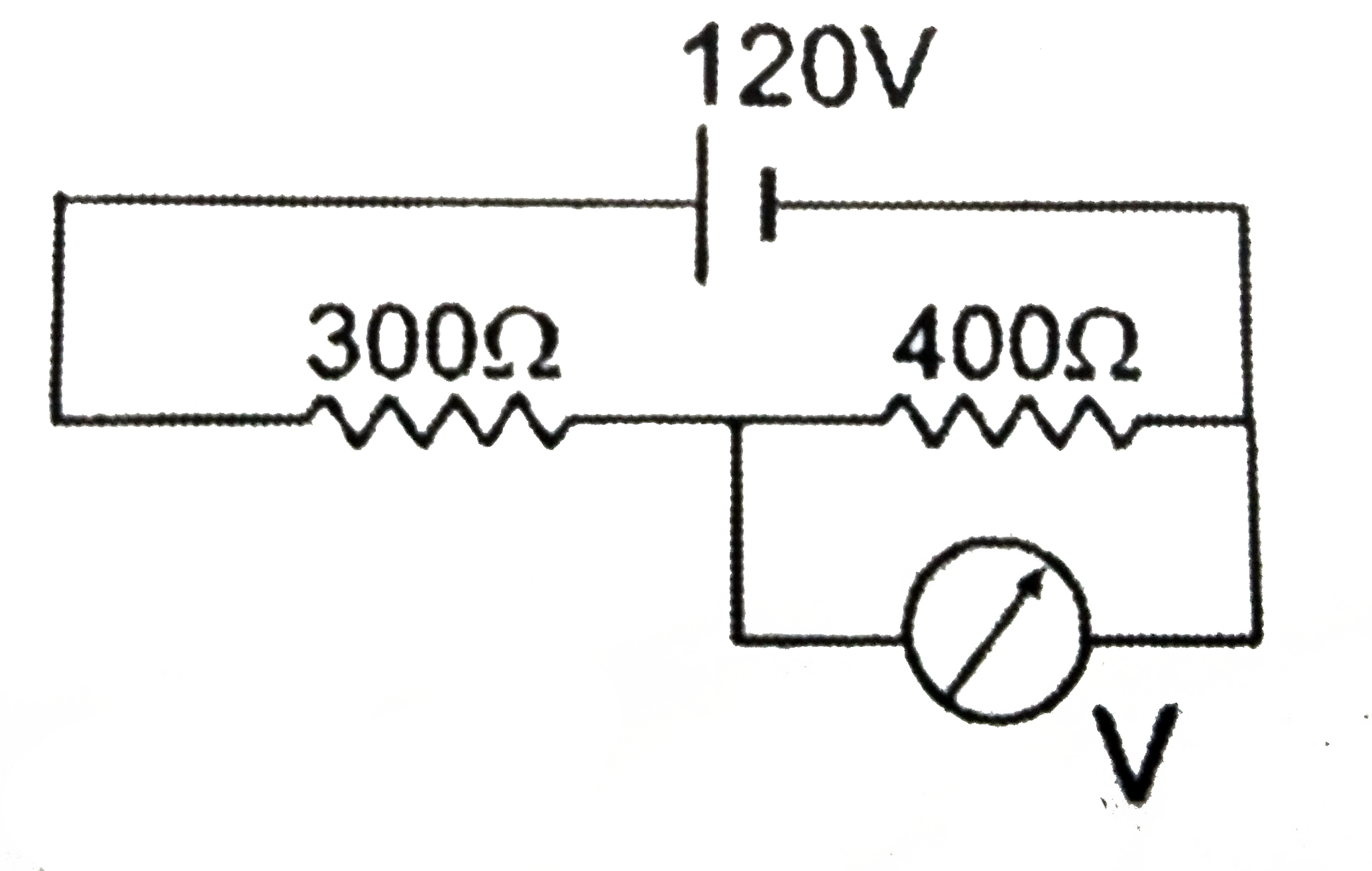 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cell which has an emf 1.5 V is connection series with an external resistance of 10Ω. If the potential difference across the cell is 1.25 V, then the internal resistance of the cell is (inΩ)
A2B0.25C1.5D0.3 - Question 2 - Select One
The voltmeter reads 40V across 60Ω resistance. The resistance of voltmeter is.
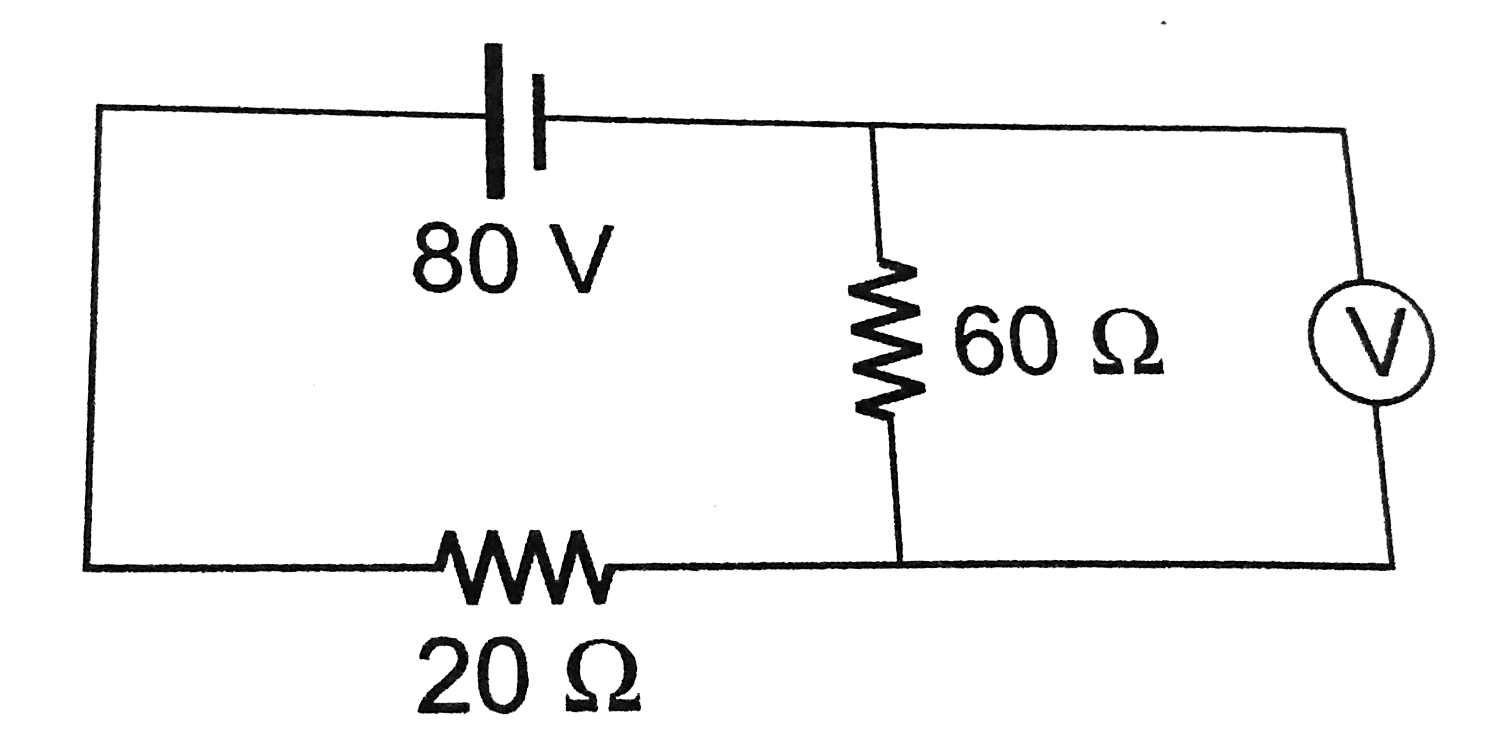 .A10ΩB20ΩC30ΩD40Ω
.A10ΩB20ΩC30ΩD40Ω - Question 3 - Select One
If 8 cells having an emf of 1.5 V are connected in series across a load having resistance of 10Ω. What is the current drawn by the load ? Assume internal resistance of all be 0.5Ω.
A0.234 AB0.632 AC0.857 ADNone of these
Three identical cells each of emf 2 V and unknown internal resistance are connected in parallel. This combination is connected to a 5Ω resistor. If the terminal voltage across the cells is 1.5 V, what is the internal resistance of each cell ?
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View SolutionA galvanometer together with an unkonwn resistance in series is connected across two identical cells, each of emf 1.5 V. When the cells are connected inseries, the galvanometer records a current of 1 A and when the cells are connected in parallel, the current =0.6 A. What is the internal resistance of each cell ?
View SolutionIn Fig.6.59, when an ideal voltmetre is connected across 4000Ω resistance, it reads 30V. If the voltmeter is connected across 3000Ω resistance, it will read
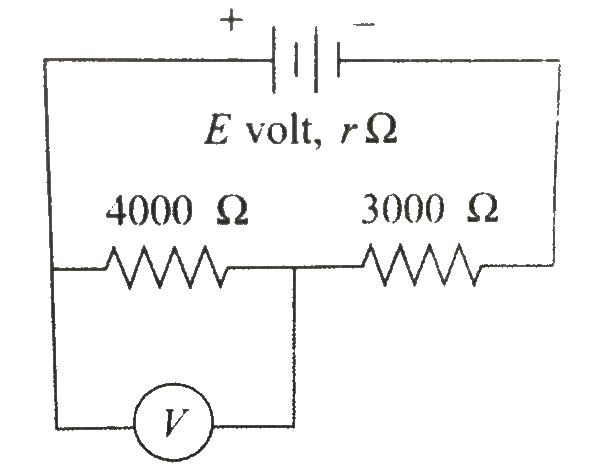 View Solution
View SolutionIn a mixed grouping of identical cells, five rows are connected in parallel and each row contains 10 cells. This combination sends a current I through an external resistance of 20Ω. if the emf and internal resistance of each cell is 1.5 V and 1Ω, respectively then find the value of I.
View Solution

