Let z be a complex number satisfying ${| z |}^{3} + 2 z^{2} + 4 ¯ z - 8 = 0$ , where $¯ z$ denotes the complex conjugate of z . Let the imaginary part of z be nonzero
Match each entry in List-I to the correct entries in List-II.

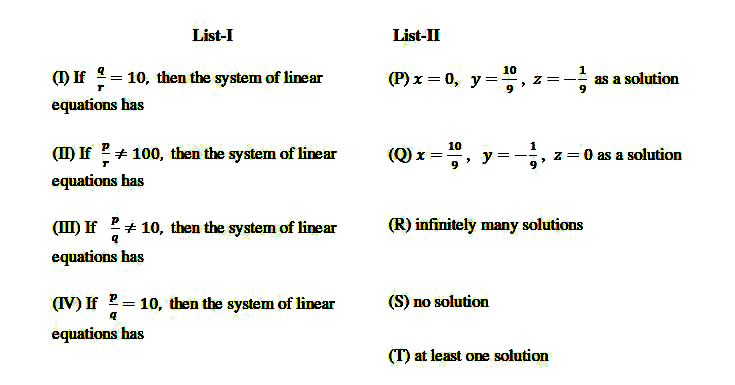
The correct option is:

$(P) \to (1) (Q) \to (4) (R) \to (5) (S) \to (4)$

$(P) \to (2) (Q) \to (1) (R) \to (3) (S) \to (5)$

$(P) \to (2) (Q) \to (4) (R) \to (5) (S) \to (1)$

$(P) \to (2) (Q) \to (3) (R) \to (5) (S) \to (4)$

Video Solution

Answer

Step by step video solution for Let z be a complex number satisfying |z|^3 +2z^2 +4barz -8 =0 , where barz denotes the complex conjugate of z . Let the imaginary part of z be nonzero Match each entry in List-I to the correct entries in List-II. The correct option is: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS JEE ADVANCED 2023

Topper's Solved these Questions

Knowledge Check

Let $z$ be a complex number satisfying $| z + 16 | = 4 | z + 1 |$ . Then
A $| z | = 4$
B $| z | = 5$
C $| z | = 6$
D $3 < | z | < 68$
z is a complex number satisfying $z^{4} + z^{3} + 2 z^{2} + z + 1 = 0$ , then $| z |$ is equal to
A $\frac{1}{2}$
B $\frac{3}{4}$
C1
Dnone of these
If z is a complex number satisfying ${| z |}^{2} + 2 (z + 2) + 3 i (z - ¯ z) + 4 = 0$ , then complex number $z + 3 + 2 i$ lies on
Acircle witih center 1-5i and radius 4
Bcircle with center 1+5i and radius 4
Ccircle with center 1+5i and radius 3
Dcircle with center 1-5i and radius 3

JEE ADVANCED PREVIOUS YEAR-JEE ADVANCED 2023-Question

Home
Ask Doubt
Profile

Let z be a complex number satisfying |z|3+2z2+4¯z−8=0 , where ¯z denotes the complex conjugate of z . Let the imaginary part of z be nonzero Match each entry in List-I to the correct entries in List-II. The correct option is:

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let z be a complex number satisfying |z+16|=4|z+1|. Then

z is a complex number satisfying z4+z3+2z2+z+1=0, then |z| is equal to

If z is a complex number satisfying |z|2+2(z+2)+3i(z−¯z)+4=0, then complex number z+3+2i lies on

JEE ADVANCED PREVIOUS YEAR-JEE ADVANCED 2023-Question

Let z be a complex number satisfying ${| z |}^{3} + 2 z^{2} + 4 ¯ z - 8 = 0$ , where $¯ z$ denotes the complex conjugate of z . Let the imaginary part of z be nonzero
Match each entry in List-I to the correct entries in List-II.

The correct option is:

Let $z$ be a complex number satisfying $| z + 16 | = 4 | z + 1 |$ . Then

z is a complex number satisfying $z^{4} + z^{3} + 2 z^{2} + z + 1 = 0$ , then $| z |$ is equal to

If z is a complex number satisfying ${| z |}^{2} + 2 (z + 2) + 3 i (z - ¯ z) + 4 = 0$ , then complex number $z + 3 + 2 i$ lies on