A particle of charge ' "-q" ' and mass ' "m" ' moves in a circle of radius ' "r" ' around an infinitely long line charge of linear charge density ' +λ '.Then time period will be given as :
(Consider "k" as Coulomb's constant)
T=2πr√m2kλq
T=12π√2kλqm
T=12πr√m2kλq
T2=4π2m2kλqr3
The correct Answer is:D
To find the time period T of a particle of charge −q and mass m moving in a circle of radius r around an infinitely long line charge with linear charge density +λ, we will follow these steps:
Step 1: Determine the Electric Field
The electric field E created by an infinitely long line charge with linear charge density λ at a distance r from the line charge is given by the formula:
E=λ2πϵ0r
Step 2: Calculate the Electric Force on the Particle
The electric force F acting on the particle due to the electric field is given by:
F=qE
Since the charge of the particle is −q, we have:
F=−q(λ2πϵ0r)=−qλ2πϵ0r
Step 3: Set the Electric Force Equal to Centripetal Force
For the particle to move in a circular path, the electric force must provide the necessary centripetal force. The centripetal force Fc is given by:
Fc=mv2r
Setting the magnitudes of the electric force and centripetal force equal gives:
qλ2πϵ0r=mv2r
Step 4: Solve for Velocity v
Rearranging the equation to solve for v2:
qλ=2πϵ0mv2
v2=qλ2πϵ0m
Step 5: Relate Velocity to Angular Velocity ω
The relationship between linear velocity v and angular velocity ω is given by:
v=rω
Substituting v into the equation gives:
(rω)2=qλ2πϵ0m
Step 6: Solve for Angular Velocity ω
Taking the square root:
r2ω2=qλ2πϵ0m
ω2=qλ2πϵ0mr2
Step 7: Find the Time Period T
The time period T is related to angular velocity ω by:
T=2πω
Substituting the expression for ω:
T=2π√mr2qλ/(2πϵ0)
Simplifying gives:
T=2πr√mqλ/(2πϵ0)
Step 8: Substitute Coulomb's Constant
Using k=14πϵ0, we can express ϵ0 in terms of k:
ϵ0=14πk
Substituting this into the equation for T:
T=2πr
⎷mqλ(2π)(14πk)
This simplifies to:
T=2πr√4πkmqλ
Final Expression
Thus, the final expression for the time period T is:
T=2πr√4πkmqλ
The electric field E created by an infinitely long line charge with linear charge density λ at a distance r from the line charge is given by the formula:
The electric force F acting on the particle due to the electric field is given by:
For the particle to move in a circular path, the electric force must provide the necessary centripetal force. The centripetal force Fc is given by:
Rearranging the equation to solve for v2:
The relationship between linear velocity v and angular velocity ω is given by:
Taking the square root:
The time period T is related to angular velocity ω by:
Using k=14πϵ0, we can express ϵ0 in terms of k:
⎷mqλ(2π)(14πk)
Thus, the final expression for the time period T is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
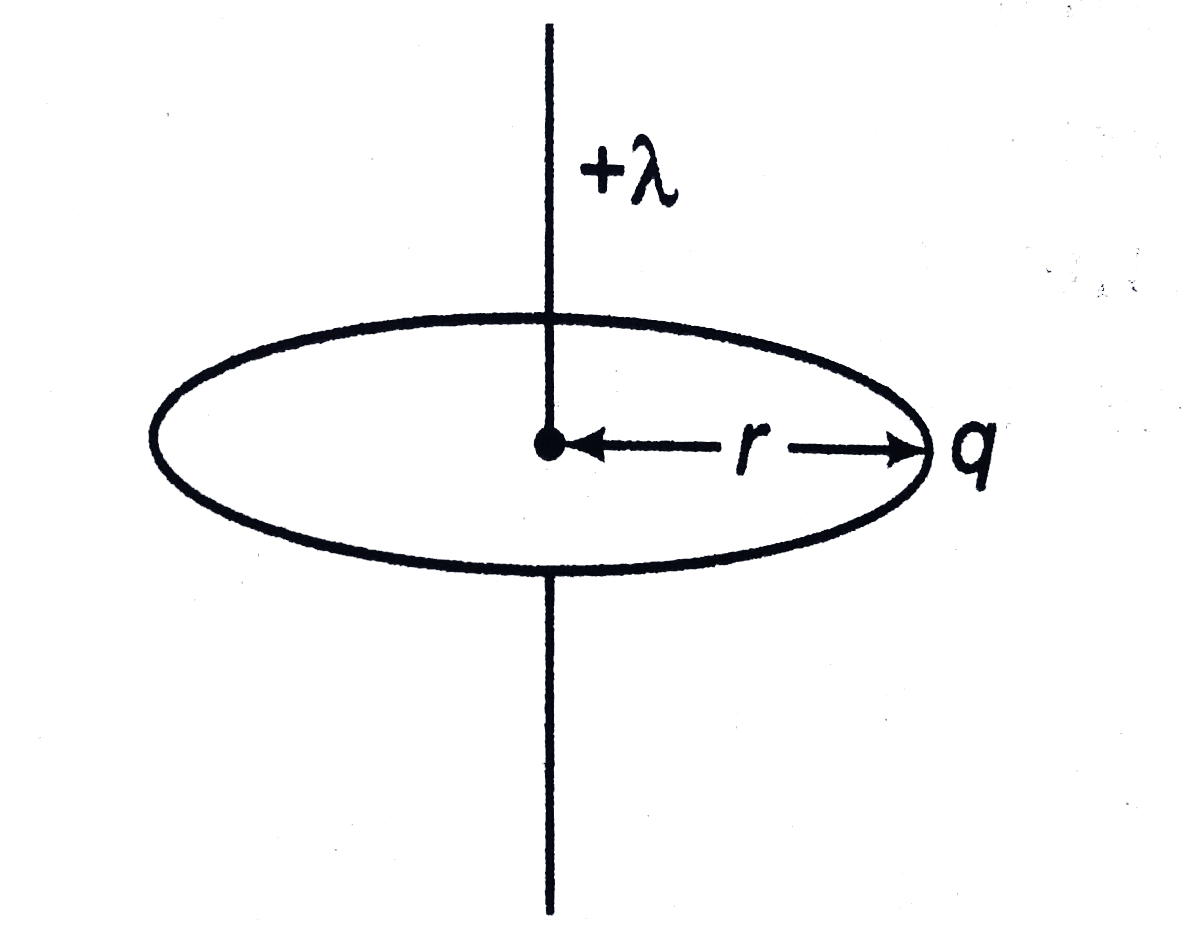 where , k=14πε0)AT=2πr√(m2kλqBT2=4π2m2kλqr3CT=12πr√2kλwmDT=12πr√m2kλq
where , k=14πε0)AT=2πr√(m2kλqBT2=4π2m2kλqr3CT=12πr√2kλwmDT=12πr√m2kλq - Question 2 - Select One
A particle of charge −q and mass m moves in a circular orbits of radius r about a fixed charge +Q.The relation between the radius of the orbit r and the time period T is
Ar=Qq16π2ε0MT3Br3=Qq16π2ε0MT2Cr2=Qq16π3ε0mT3Dr2=Qq16π3ε0mT3 - Question 3 - Select One
Consider an infinite line charge having uniform linear charge density and passing through the axis of a cylinder is removed.
 AdecreaseBincreasesCremains sameDcannot say
AdecreaseBincreasesCremains sameDcannot say
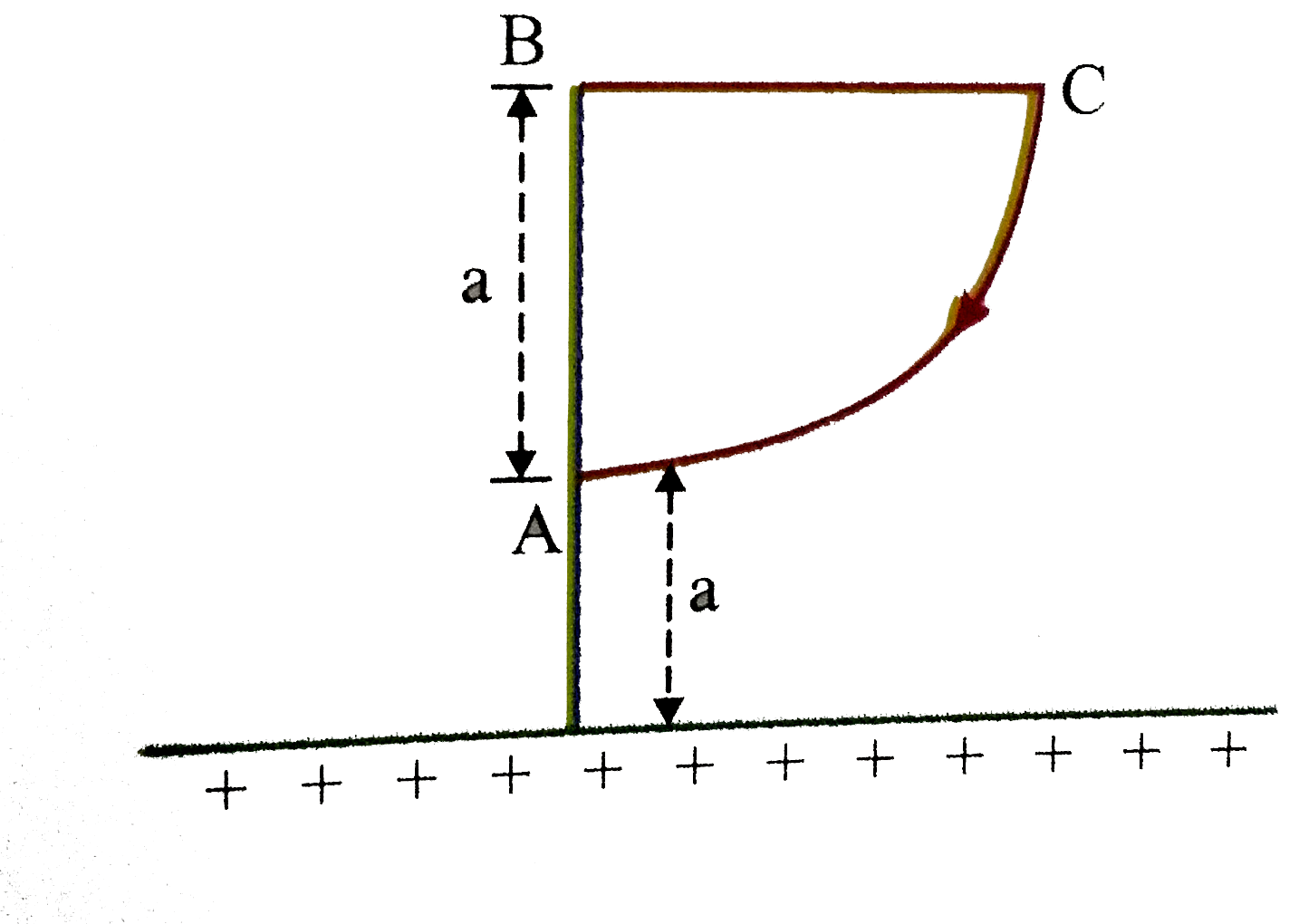
Find the electric field at the origin due to the line charge (ABCD) of linear charge density λ,
 View Solution
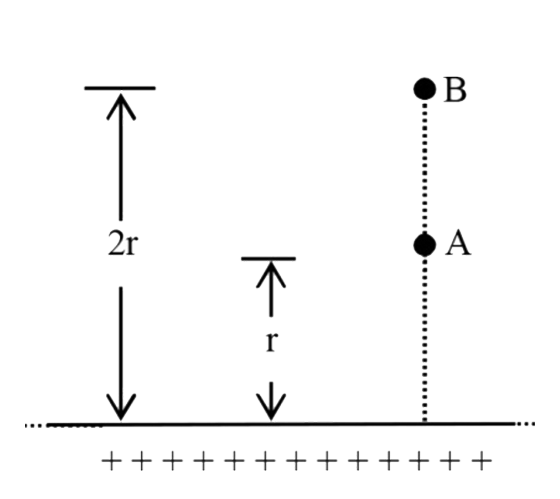
View SolutionAn infinitely long line of linear charge density λ is shown in the figure. The potential difference VA−VB between the two points A and B is
 View Solution
View SolutionOn rotating a point charge g around a charge Q in a circle of radius r, the work done is
View SolutionFor an infinite line of charge having linear charge density λ lying along x-axis the work done in moving a charge q form C to A along CA is
 View Solution
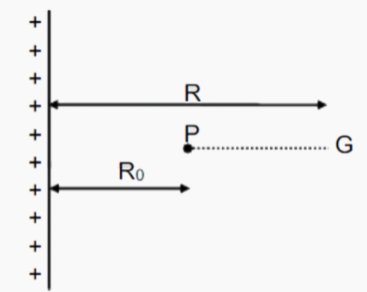
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
 View Solution
View Solution

