A block of mass "m" is placed on a surface having vertical crossection given by y=x24.If coefficient of friction is "0.5" ,the maximum height above the ground at which block can be placed without slipping is:
1/3 m
1/4 m
1/6 m
1/2 m
To solve the problem, we need to determine the maximum height at which a block of mass m can be placed on a surface defined by the equation y=x24 without slipping, given that the coefficient of friction μ=0.5.
1. Understand the Surface Equation:
The surface is defined by the equation y=x24. This is a parabolic curve that opens upwards.
2. Determine the Slope of the Surface:
The slope of the surface at any point can be found by differentiating y with respect to x:
dydx=ddx(x24)=2x4=x2
This slope represents tanθ, where θ is the angle of inclination of the surface.
3. Apply the Condition for No Slipping:
For the block to not slip, the frictional force must be sufficient to counteract the component of gravitational force acting down the slope. The condition for no slipping can be expressed as:
μmgcosθ≥mgsinθ
Dividing through by mg (assuming m≠0):
μcosθ≥sinθ
Rearranging gives:
μ≥tanθ
4. Substituting the Slope into the Condition:
Since tanθ=dydx=x2, we substitute this into the inequality:
0.5≥x2
Multiplying both sides by 2:
1≥x
This implies:
x≤1
5. Finding the Corresponding Height:
Now, we need to find the maximum height y when x=1:
y=x24=124=14
6. Conclusion:
The maximum height above the ground at which the block can be placed without slipping is:
14 meters
The surface is defined by the equation y=x24. This is a parabolic curve that opens upwards.
The slope of the surface at any point can be found by differentiating y with respect to x:
dydx=ddx(x24)=2x4=x2
This slope represents tanθ, where θ is the angle of inclination of the surface.
For the block to not slip, the frictional force must be sufficient to counteract the component of gravitational force acting down the slope. The condition for no slipping can be expressed as:
μmgcosθ≥mgsinθ
Dividing through by mg (assuming m≠0):
μcosθ≥sinθ
Rearranging gives:
μ≥tanθ
Since tanθ=dydx=x2, we substitute this into the inequality:
0.5≥x2
Multiplying both sides by 2:
1≥x
This implies:
x≤1
Now, we need to find the maximum height y when x=1:
y=x24=124=14
The maximum height above the ground at which the block can be placed without slipping is:
14 meters
Topper's Solved these Questions
Similar Questions
A block of mass 'm' is placed on a rough surface with a vertical cross section of y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is .
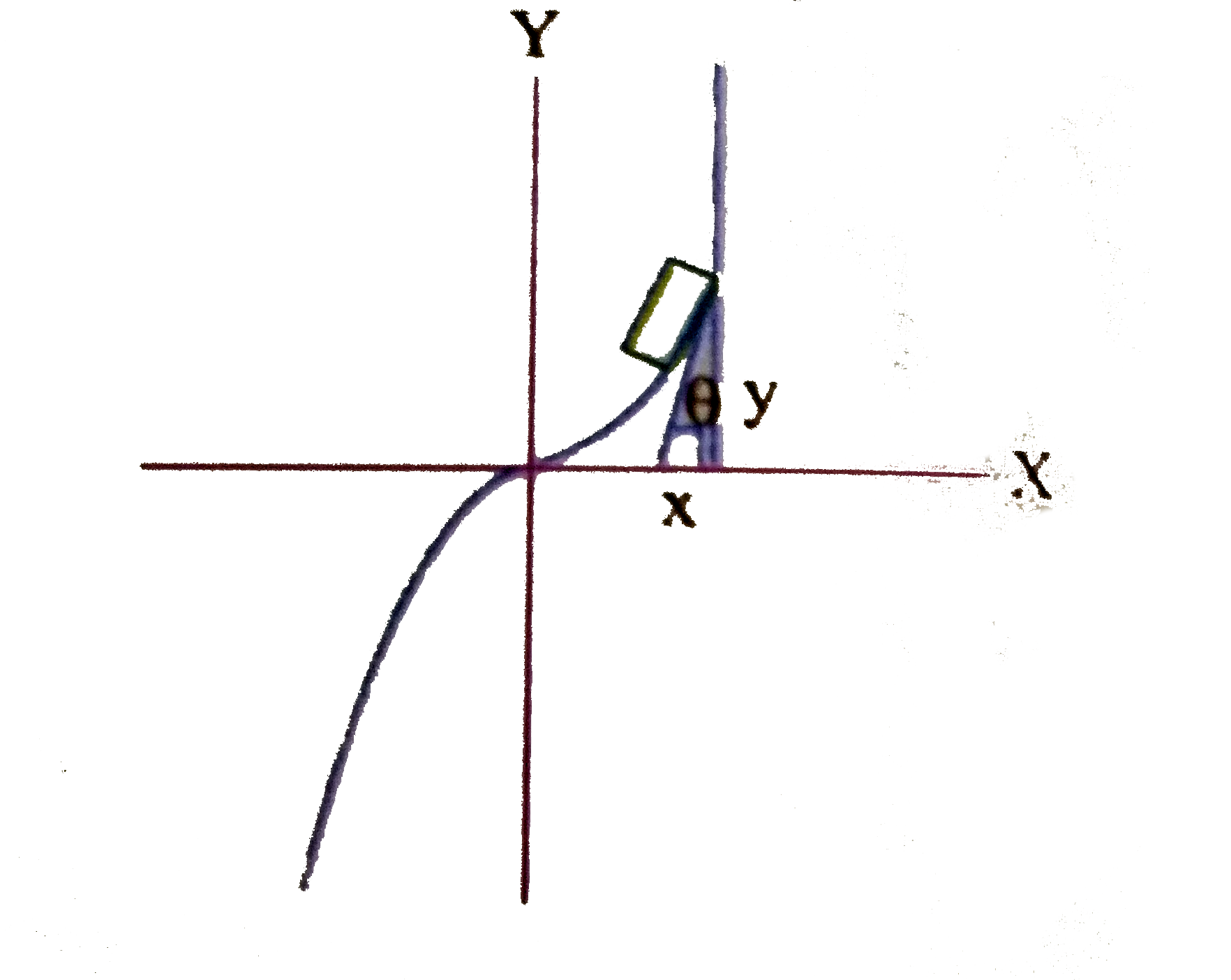
View SolutionA block of mass m is palced on a surface having coefficient of frictionn 0.25, with a vertical cross section given by y=x416. Calculate the maximum height above the ground t which block can be placed without slipping.
View Solution
Knowledge Check
A block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
A(a) 16mB(b) 23mC(c) 13mD(d) 12mA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNoneA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isAμgBμMmgCμmMgDgμ
A spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
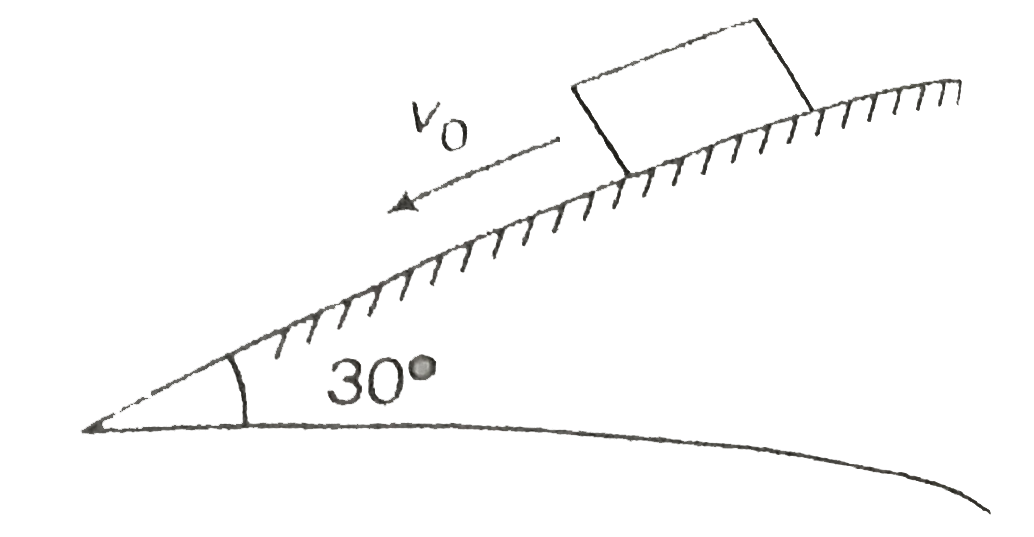
View SolutionA block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will
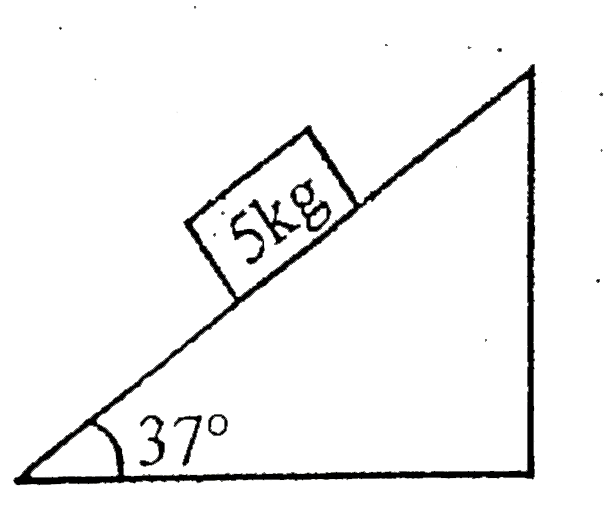
View SolutionA block of mass "5kg" is placed on a wedge having inclination of 37∘ with the horizontal. Coefficient of friction between block and wedge is 0.8. Then select the correct statement.
View SolutionA block of mass m=2kg is placed in equilibrium on a moving plank accelerating with a=4m/s2 . If coefficient of friction between plank and block μ=0.2 . The friction force acting on the block is:
View SolutionA block of mass m=2kg is placed in equilibrium on a moving plank accelerating with a=1m/s2 . If coefficient of friction between plank and block μ=0.2 . The friction force acting on theblock is:
View Solution
