If the total energy transferred to a surface in time "t" is 6.48×105J ,then the magnitude of the total momentum delivered to this surface for complete absorption will be:
2.16×10−3kgm/s
2.46×10−3kgm/s
1.58×10−3kgm/s
4.32×10−3kgm/s
To find the magnitude of the total momentum delivered to a surface for complete absorption of energy, we can use the relationship between energy (E) and momentum (p) in the context of light or electromagnetic radiation. The relevant formula is:
p=Ec
where:
- p is the momentum,
- E is the energy transferred,
- c is the speed of light in a vacuum, approximately 3×108 m/s.
1. Identify the Given Values:
- Total energy transferred, E=6.48×105 J
- Speed of light, c=3×108 m/s
2. Use the Formula for Momentum:
Substitute the values into the momentum formula:
p=Ec=6.48×105 J3×108 m/s
3. Perform the Calculation:
- First, calculate the division:
p=6.483×105108
- Simplifying 105108 gives 10−3:
p=6.483×10−3
- Now calculate 6.483:
6.483=2.16
- Therefore:
p=2.16×10−3 kg m/s
4. Final Result:
The magnitude of the total momentum delivered to the surface for complete absorption is:
p=2.16×10−3 kg m/s
Conclusion:
The answer to the question is 2.16×10−3 kg m/s, which corresponds to the first option provided in the question.
- p is the momentum,
- E is the energy transferred,
- c is the speed of light in a vacuum, approximately 3×108 m/s.
- Total energy transferred, E=6.48×105 J
- Speed of light, c=3×108 m/s
Substitute the values into the momentum formula:
p=Ec=6.48×105 J3×108 m/s
- First, calculate the division:
p=6.483×105108
- Simplifying 105108 gives 10−3:
p=6.483×10−3
- Now calculate 6.483:
6.483=2.16
- Therefore:
p=2.16×10−3 kg m/s
The magnitude of the total momentum delivered to the surface for complete absorption is:
p=2.16×10−3 kg m/s
The answer to the question is 2.16×10−3 kg m/s, which corresponds to the first option provided in the question.
Topper's Solved these Questions
Similar Questions
Light with an energy. fiux of 20W(cm)2 falls on a nonreflecting surface at normal incidence. If the surface has an area of 30cm2, the total momentum delivered (for complete absorption) during 30 min is n×10−4kgms−1, then find n.
View SolutionThe total surface area of a cube of an edge 10 cm is
View Solution
Knowledge Check
If the total electromagnetic energy falling on a surface is U then the total momentum delivered (for complate absorption) is
AU/cBcUCU/c2Dc2ULight with an energy flux20W/cm2 falls on a non-reflecting surface at normal incidence. If the surface has an area of 30cm2. the total momentum delivered ( for complete absorption)during 30 minutes is
A36×105kg−m/sB36×104kg−m/sC1.08×104kg−m/sD1.08×107kg−m/sLight is incident normally on a completely absorbing surface with an energy flux of 25Wcm−2 If the surface has an area of 25cm2 the momentum transferred to the surface in 40 min time duration will be:
A6.3×10−4NsB5.0×10−3NsC1.4×10−6NsD3.5×10−6Ns
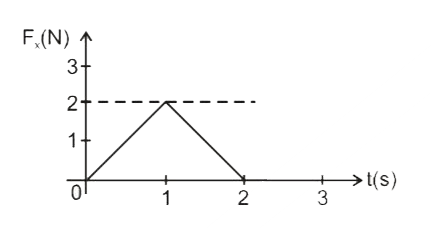
The given figure shows a plot of the time dependent force Fx acting on a particle in motion along the x-axis. What is the total impulse delivered by this force to the particle from time t = 0 to t = 2second?
View SolutionCalculate the momentum transferred to a surface when a radiation of energy E falls normally on it. Assume that the reflectivity of the surface is unity.
View SolutionCalcuate the momentum transferred to a surface when a radiation of energy E falls normally on it. Assume that the reflectivity of the surface is unity.
View SolutionCalculate the momentum transferred to a surface when a radiation of energy E falls normally on it. Assume that the reflectivity of the surface is unity.
View SolutionIf En and Ln denote the total energy and the angular momentum of an electron in the nth orbit of Bohr atom, then
View Solution