The ratio of velocity of two objects A and B is 1:3. It the position-time graph of object A is inclined to time axis at 30∘, then the position-time graph of object B is inclined to time axis at
0∘
90∘
30∘
60∘
The correct Answer is:D
To solve the problem, we need to analyze the given information about the velocities of two objects A and B and their position-time graphs.
1. Understanding the Ratio of Velocities:
We are given that the ratio of the velocities of objects A and B is VA:VB=1:3. This means:
VA=kandVB=3k
for some constant k.
2. Analyzing Object A's Position-Time Graph:
The position-time graph of object A is inclined at an angle of 30∘ to the time axis. The slope of a position-time graph gives the velocity of the object. Therefore, we can express the velocity of object A in terms of the angle:
VA=slope=tan(30∘)=1√3
3. Finding the Velocity of Object B:
Since we have VA=1√3, we can find VB using the ratio:
VB=3⋅VA=3⋅1√3=√3
4. Determining the Angle for Object B's Position-Time Graph:
The slope of the position-time graph for object B will also give us its velocity:
VB=tan(θB)
where θB is the angle of inclination of object B's graph. We know:
VB=√3
Therefore:
tan(θB)=√3
5. Finding the Angle θB:
The angle θB for which tan(θB)=√3 is:
θB=60∘
6. Conclusion:
The position-time graph of object B is inclined to the time axis at 60∘.
Final Answer:
The position-time graph of object B is inclined to the time axis at 60∘.
---
We are given that the ratio of the velocities of objects A and B is VA:VB=1:3. This means:
VA=kandVB=3k
for some constant k.
The position-time graph of object A is inclined at an angle of 30∘ to the time axis. The slope of a position-time graph gives the velocity of the object. Therefore, we can express the velocity of object A in terms of the angle:
VA=slope=tan(30∘)=1√3
Since we have VA=1√3, we can find VB using the ratio:
VB=3⋅VA=3⋅1√3=√3
The slope of the position-time graph for object B will also give us its velocity:
VB=tan(θB)
where θB is the angle of inclination of object B's graph. We know:
VB=√3
Therefore:
tan(θB)=√3
The angle θB for which tan(θB)=√3 is:
θB=60∘
The position-time graph of object B is inclined to the time axis at 60∘.
The position-time graph of object B is inclined to the time axis at 60∘.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - B)19videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)7videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself40videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
Similar Questions
Knowledge Check
- Question 1 - Select One
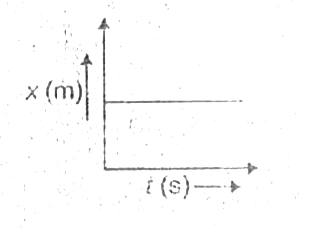
Look at the given distance -time graph of an object .
 AThe speed of the object is increasing continuously.BThe speed of the object is decreasing continuously.CThe speed of the object is constant.DThe acceleration of the object is zero.
AThe speed of the object is increasing continuously.BThe speed of the object is decreasing continuously.CThe speed of the object is constant.DThe acceleration of the object is zero. - Question 2 - Select One
The position-time graph of an object is a straight line parallel to time axis. This implies that the object is
AMoving with uniform accelerationBMoving with uniform velocityCMoving with non-uniform velocityDStationary
The position-time graph of an object is given below. What is the velocity of the object?
 View Solution
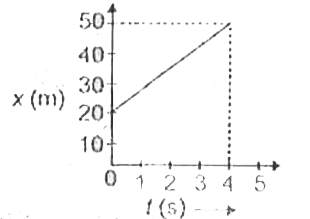
View SolutionThe position - time graph of an object is given below. What is the velocity of the object?
 View Solution
View SolutionThe position - time graph of an object is given below. What is the velocity of the object?
 View Solution
View SolutionDraw the position-time graph for an object in uniform motion. Show that the slope of the position-time graph gives the velocity of the object.
View SolutionDraw the position-time graph of an object moving with positive accceleration.
View SolutionThe x-t graph of an object is a straight line inclined to time-axis. What does this statement indicate ?
View Solution


