Light falls at normal incidence on one face of a glass prism of refractive index 1.5, what will be the angle of emergence when the angle of the prism is (a) $30^{\circ}$ (b) $50^{\circ}$ ?

Video Solution

Text Solution

Verified by Experts

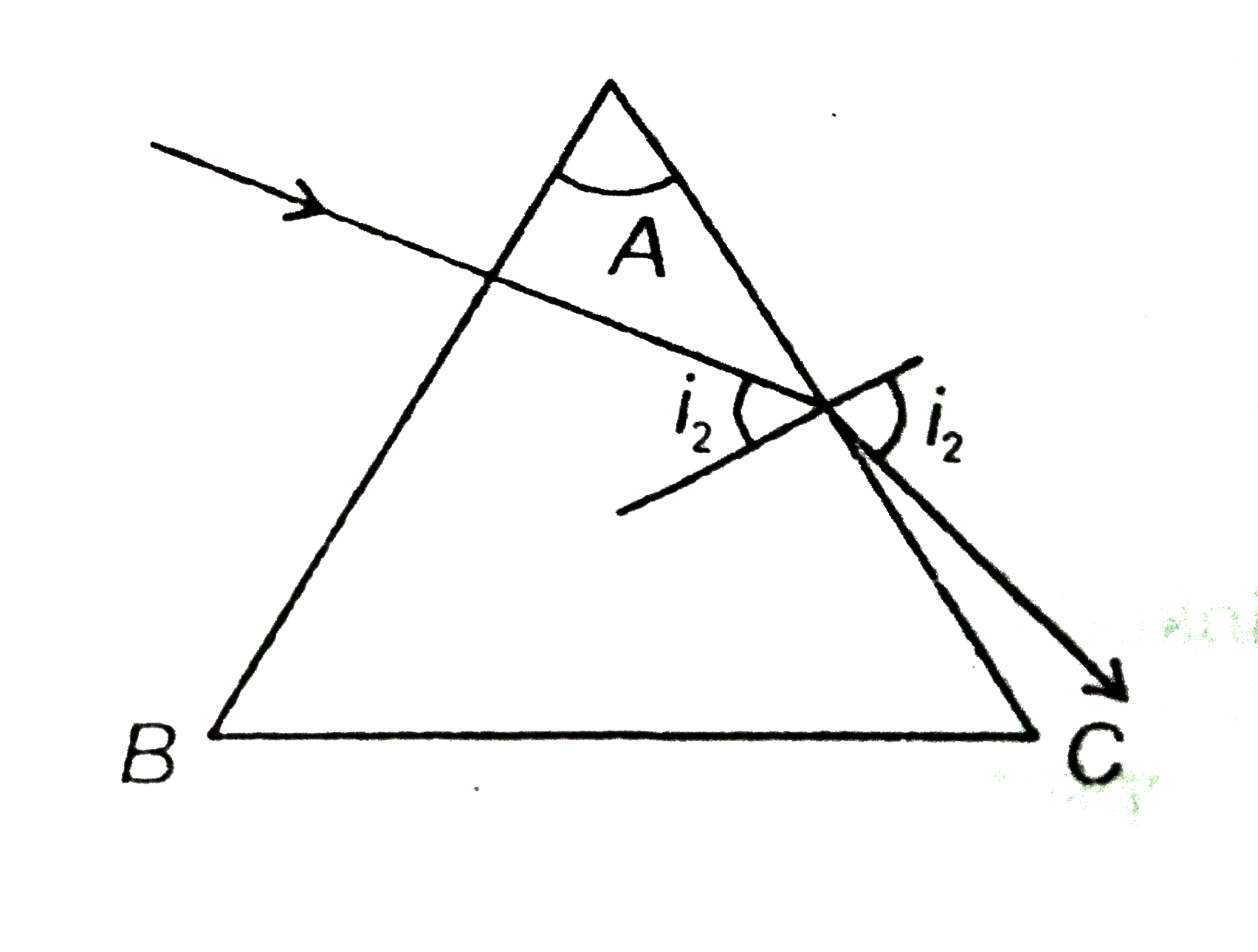
The incident ray is normal to the face AB of the prism shown in the figure. So, the angle of incidence, $i_{1} = 0$ making $r_{1} = 0$
When light undergoes refraction through a prism, $r_{1} + r_{2} = A$
(a) $0 + r_{2} = 30^{\circ}$
$r_{2} = 30^{\circ}$
${sin i}_{2} = μ {sin r}_{2} = 1.5 {sin 30}^{\circ} = 1.5 (0.5) = 0.75$
(b) $A = 50^{\circ}$
Substituting in $r_{1} + r_{2} = A$
$0 + r_{2} = 50^{\circ}, r_{2} = 50^{\circ}$
${sin i}_{2} = μ {sin r}_{2} = 1.5 {sin 50}^{\circ} = 1.5 (0.7660) = 1.149$
No value of $i_{2}$ can satisfy this relation. So, there is not refraction at the second surface i.e., there is no emergent ray from the face AC of the prism. The light is totally reflected as $r_{2}$ is greater than the critical angle.

Updated on:21/07/2023

Light falls at normal incidence on one face of a glass prism of refractive index $\sqrt{2}$ . Then the angle of emergence when the angle of the prism is $45^{\circ}$
A45°
B60°
C15°
D90°
A ray of light is incident normally on one of the equal faces of a right isosceles prism of refractive index 1.5. The angle between incident and emergent rays is
A $45^{\circ}$
B $90^{\circ}$
C $180^{\circ}$
D $0^{\circ}$
The least angle of deviation for a glass prism is equal to its refracting angle. The refractive index of glass is 1.5. Then the angle of the prism is
A $2 {cos}^{- 1} (\frac{3}{4})$
B ${sin}^{- 1} (\frac{3}{4})$
C ${sin}^{- 1} (\frac{3}{2})$
D ${cos}^{- 1} (\frac{3}{2})$