PP' and QQ' are two direct common tangents at two circles intersecing in point A and B.The common chord produced intersects PP' in R and QQ' in S. prove that RS2=PP'2+AB2
Power of circle
RP2=RA⋅RB
RP'2=RA⋅RB
RP2=RP'2
RP=RP'
PP'=RP+RP'
RP=RP'=12PP'
RS2−AB2=(RS+AB)(RS−AB)
=(RA+BS+2AB)(RA+BS)
=(2RA+2AB)(2RA)
=4(RB⋅RA)
RS2−AB2=4RP2
=4(12PP')2
RS2−AB2=4⋅14(PP')2
RS2=PP'2+AB2.
Similar Questions
CD is direct common tangent to two circles intersecting each other at A and B. The ∠CAD+∠CBD is equal to
 View Solution
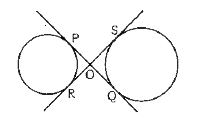
View SolutionIn the figure, PQ and RS are the common tangents to two circles intersecting at O.
Prove that PQ=RS
 View Solution
View SolutionCommon tangents AB and CD to two circles intersects at E. Prove that AB=CD
View SolutionIn figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.
 View Solution
View SolutionIn figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.
 View Solution
View SolutionCommon Tangents of Two Circles - Direct and Transverse Common Tangent
View SolutionIn Figure, common tangents PQandRs to two circle intersect at A. Prove that PQ=RS.
View SolutionIn Figure, common tangents P Q and RS to two circle intersect at A. Prove that PQ=RS
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.
 View Solution
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.
 View Solution
View Solution

