ABCD is a rectangle with sides AB=p,BC=q. If AB and AD are taken as negative directions of coordinate axes, then the equation of the circle circumscribing the rectangle is
Step by step video & image solution for ABCD is a rectangle with sides AB = p, BC = q. If AB and AD are taken as negative directions of coordinate axes, then the equation of the circle circumscribing the rectangle is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
ABCD is a rectangle wih sides AB=p, BC=q,. If AB and AD are taken negative directions of coordinate axes. then the equaton of the circumscribing the rectangle is
View SolutionABCD is a square with side a. If AB and AD are taken as positive coordinate axes then equation of circle circumscribing the square is
View Solution
Knowledge Check
ABCD is a square, the length of whose side is a. Taking AB and AD as the coordinate axes, the equation of the circel passing through the ceteices of the square is
Ax2+y2+ax+ay=0Bx2+y2−ax−ay=0Cx2+y2+1ax+2ay=0Dx2+y2−2ax−2ay=0ABCD is a rectangle in which AB - BC = 1 cm. If area of rectangle is 20cm2, then its perimeter will be
A16 cmB20 cmC18 cmD25 cmABCD is a square of side a. The centre of the circle which circumscribes the square on taking AB and AD as axes is
A(a, -a)B(-a, a)C(1/2,a/2)Dnone
Construct a rectangle ABCD whose sides AB=5.4 cm and BC=4.5cm.
View SolutionLet ABCD be a rectangle such that AB=10 units and BC=8 units. Taking AB and AD as x and y axis respectively, find the coordinates of A, B, C and D.
View SolutionLet ABCD be a rectangle such that AB=10 units and BC=8 units. Taking AB and AD as x and y axis respectively, find the coordinates of A, B, C and D.
View SolutionIn the figure, ABCD is a rectangle and E is a point on the side AB. If AB=10andAD=5 what is the area of the shaded region in the figure?
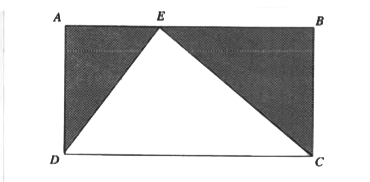
View SolutionABCD is a rectangle with A(−1,2),B(3,7) and AB:BC=4:3. If P is the centre of the rectangle, then the distance of P from each corner is equal to
View Solution
