ABCD is a square with side a. If AB and AD are taken as positive coordinate axes then equation of circle circumscribing the square is
x2+y2−ax−ay=0
x2+y2+ax+ay=0
x2+y2−ax+ay=0
x2+y2+ax−ay=0
The correct Answer is:A
To find the equation of the circle circumscribing the square ABCD with side length a, where AB and AD are taken as positive coordinate axes, we can follow these steps:
Step 1: Identify the coordinates of the square's vertices
Since AB and AD are on the positive axes, we can place the square in the coordinate plane as follows:
- A(0,0)
- B(a,0)
- C(a,a)
- D(0,a)
Step 2: Find the center of the circle
The center of the circle that circumscribes the square is the midpoint of the diagonal connecting opposite corners. The coordinates of the center O can be calculated as:
O(0+a2,0+a2)=O(a2,a2)
Step 3: Calculate the radius of the circle
The radius R of the circumscribing circle is the distance from the center O to any vertex of the square. We can use the distance formula to find this:
R=√(a−a2)2+(0−a2)2
Calculating this gives:
R=√(a2)2+(−a2)2=√a24+a24=√2a24=√a22=a√2
Step 4: Write the equation of the circle
The general equation of a circle with center (h,k) and radius R is given by:
(x−h)2+(y−k)2=R2
Substituting h=a2, k=a2, and R=a√2 into the equation:
(x−a2)2+(y−a2)2=(a√2)2
This simplifies to:
(x−a2)2+(y−a2)2=a22
Step 5: Expand the equation
Expanding the left side:
(x2−ax+a24)+(y2−ay+a24)=a22
Combining terms gives:
x2+y2−ax−ay+a22=a22
Subtracting a22 from both sides results in:
x2+y2−ax−ay=0
Final Result
Thus, the equation of the circle circumscribing the square ABCD is:
x2+y2−ax−ay=0
---
Since AB and AD are on the positive axes, we can place the square in the coordinate plane as follows:
- A(0,0)
- B(a,0)
- C(a,a)
- D(0,a)
The center of the circle that circumscribes the square is the midpoint of the diagonal connecting opposite corners. The coordinates of the center O can be calculated as:
O(0+a2,0+a2)=O(a2,a2)
The radius R of the circumscribing circle is the distance from the center O to any vertex of the square. We can use the distance formula to find this:
R=√(a−a2)2+(0−a2)2
Calculating this gives:
R=√(a2)2+(−a2)2=√a24+a24=√2a24=√a22=a√2
The general equation of a circle with center (h,k) and radius R is given by:
(x−h)2+(y−k)2=R2
Substituting h=a2, k=a2, and R=a√2 into the equation:
(x−a2)2+(y−a2)2=(a√2)2
This simplifies to:
(x−a2)2+(y−a2)2=a22
Expanding the left side:
(x2−ax+a24)+(y2−ay+a24)=a22
Combining terms gives:
x2+y2−ax−ay+a22=a22
Subtracting a22 from both sides results in:
x2+y2−ax−ay=0
Thus, the equation of the circle circumscribing the square ABCD is:
x2+y2−ax−ay=0
Similar Questions
ABCD is a rectangle wih sides AB=p, BC=q,. If AB and AD are taken negative directions of coordinate axes. then the equaton of the circumscribing the rectangle is
View SolutionABCD is a square in first quadrant whose side is a, taking ABandAD as axes, prove that the equation to the circle circumscribing the square is x2+y2=a(x+y).
View Solution
Knowledge Check
In the figure, O is the center of the circle of radius 3, and ABCD is a square. If PC=3 and the side BC of the square is a tangent to the circle, then what is the area of the square ABCD?
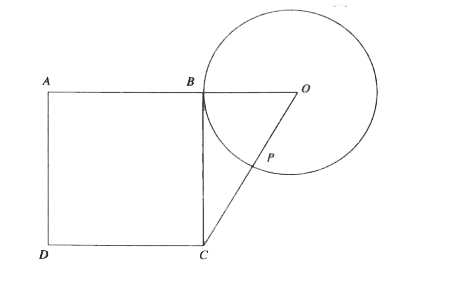 A25B27C36D42
A25B27C36D42
A circle circumscribing an equilateral triangle with centroid at (0,0) of a side a isdrawn and a square is drawn touching its four sides to circle. The equation ofcircle circumscribing the square is :
View SolutionProve that the rectangle circumscribing a circle is a square
View SolutionFigure, ABCD is a square of side 2a. Find the ratio between the circumferences and the areas of the incircle and the circum-circle of the square.
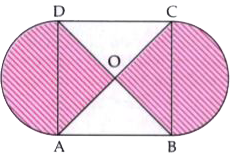
View SolutionIn the given figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semi circles are drawn with AD and BC as diameters. Find the area of the shaded region
(Take π=227)
View SolutionIf a square of side 10 is inscribed in a circle then radius of the circle is
View SolutionIn the given figure, ABCD is a square of side 7 cm. DPBA and DQBC are quardrants of circles each of the radius 7 cm. Find the area of the shaded region.

View SolutionIn the adjoining figure, ABCD is a square of side 10 cm and two semicircles with side of the square as diameter. A quarter circle is also seen in figure with side of square as radius. Find the area of the square region excluding the shaded part . (Take π=3.14)

View Solution