Let ABCD be a rectangle such that AB=10 units and BC=8 units. Taking AB and AD as x and y axis respectively, find the coordinates of A, B, C and D.
To find the coordinates of the vertices of rectangle ABCD, we can follow these steps:
Step 1: Understand the placement of the rectangle
We are given that AB = 10 units and BC = 8 units. We will place AB along the x-axis and AD along the y-axis.
Step 2: Define the coordinates of point A
Since we are placing point A at the origin, the coordinates of point A will be:
A(0,0)
Step 3: Determine the coordinates of point B
Point B is located 10 units along the x-axis from point A. Therefore, the coordinates of point B will be:
B(10,0)
Step 4: Determine the coordinates of point C
Point C is located 8 units above point B along the y-axis. Since B is at (10, 0), moving 8 units up gives us:
C(10,8)
Step 5: Determine the coordinates of point D
Point D is directly above point A along the y-axis, which means it is 8 units above the origin. Thus, the coordinates of point D will be:
D(0,8)
Summary of the coordinates
Now we can summarize the coordinates of all points:
- A(0,0)
- B(10,0)
- C(10,8)
- D(0,8)
Final Answer
The coordinates of points A, B, C, and D are:
- A: (0, 0)
- B: (10, 0)
- C: (10, 8)
- D: (0, 8)
---
We are given that AB = 10 units and BC = 8 units. We will place AB along the x-axis and AD along the y-axis.
Since we are placing point A at the origin, the coordinates of point A will be:
A(0,0)
Point B is located 10 units along the x-axis from point A. Therefore, the coordinates of point B will be:
B(10,0)
Point C is located 8 units above point B along the y-axis. Since B is at (10, 0), moving 8 units up gives us:
C(10,8)
Point D is directly above point A along the y-axis, which means it is 8 units above the origin. Thus, the coordinates of point D will be:
D(0,8)
Now we can summarize the coordinates of all points:
- A(0,0)
- B(10,0)
- C(10,8)
- D(0,8)
The coordinates of points A, B, C, and D are:
- A: (0, 0)
- B: (10, 0)
- C: (10, 8)
- D: (0, 8)
Similar Questions
ABCD is a rectangle with AB=16 units and BC=12 units. F is a point on AB and E is a point on CD such that AFCE is a rhombus. Find the length of EF.
View SolutionIn rectangle along x-axis and AB=8 units. Find the co-ordinates of vertices A,B and C.
View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.
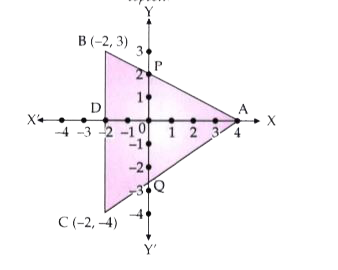
(i) Write the coordinates of A.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
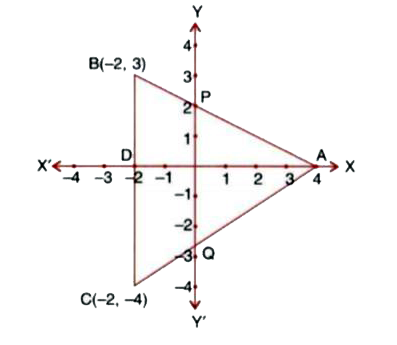
Find the length of AB and AC.
View SolutionA is a point on x- axis, and point B (5,-4) and AB = 5 units find the co-ordinates of A.
View SolutionIn rectangle OABC, point O is the origin, OA=10 units along x-axis and AB=8 units. Find the co-ordinates of vertices A,B and C.
View SolutionA circle passing through the vertex C of a rectangle ABCD and touching its sides AB and AD at M and N, respectively. If the distance from C to the line segment MN is equal to 5 units, then find the area of the reactangle ABCD.
View SolutionGiven a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
View SolutionThe line xa+yb=1 meets the axis of and y at A and B respectively and C is middle point of AB then
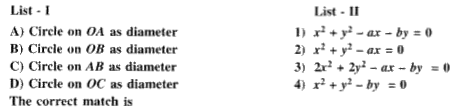
View SolutionABCD is a rectangle. A circle passing through vertex C touches the sides AB and AD at M and N respectively. If the distance lof the line MN from the vertex C is P units then the area of rectangle ABCD is
View Solution
