Figure shows the curve y=x2. Find the area of the shaded part between x=0andx=6.

Video Solution
Text Solution
The area can be divided into strips by drawing ordiN/Ates between x=0 and x=6 at a regular interval of dx. Cionsider the strip between the oridiN/Ates at x and x+dx. The height of this strip is y=x2. The area of this strip is dA=ydx=x2dx.
The total area of the shaded part is obtained by suming up these strip areas with x varying from o0 to 6. Thus,
A=∫6_0x2dx
=[x33]6_0=216−03=72
|
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBook:HC VERMAChapter:PHYSICS AND MATHEMATICSExercise:Short Answer
Explore 14 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMAChapter:PHYSICS AND MATHEMATICSExercise:Objective 1
Explore 6 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMAChapter:PHYSICS AND MATHEMATICSExercise:Exercises
Explore 34 Videos
- NEWTON'S LAWS OF MOTIONBook:HC VERMAChapter:NEWTON'S LAWS OF MOTIONExercise:Exercises
Explore 42 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMAChapter:REST AND MOTION : KINEMATICSExercise:Exercises
Explore 51 Videos
Similar Questions
Knowledge Check
Find the area bounded by the curve y =sin x between x=0 and x=2π.
A1 sq unitB2 sq unitsC3 sq unitsD4 sq unitsFind the area of region by the curve y=sinx between x=0 and x=2π.
A5 sq unitsB4 sq unitsC3 sq unitsD7 sq units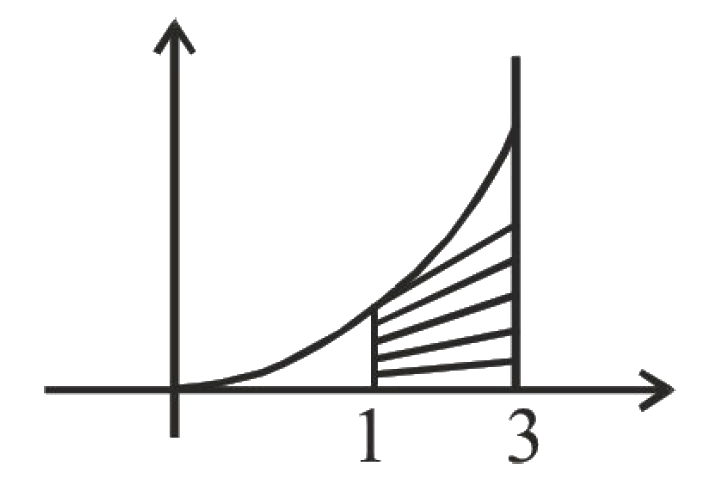
Find the area under the shaded region for curve y=3x2.A80B26C20D40
Find the area bounded by the curve y=sinxbetweenx=0andx=2π.
View SolutionFind the area bounded by the curve y=sinx between x=0 and x=2π.
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionFind the area of region by the curve y=sinx between x=0 and x=2π.
View SolutionFind the area enclosed the curve y=sin x and the X-axis between x=0andx=π.
View Solution