Both the springs shown in figure are untretched. If the block is displaced by a distance x and released, what will be the initial acceleration?
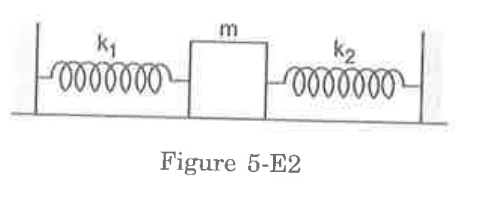
Given, x=20cm=0.2m,
k=15Nm,m=0.3kg
Ae≤ration,a=Fm=−kxm=−15(0.2)0.3
= - 3/0.3 = - 10 m/s^2
(deceleration),
So, the acceleration is 10 m/s^2 opposite to the direction of motion.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective 2
9 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions

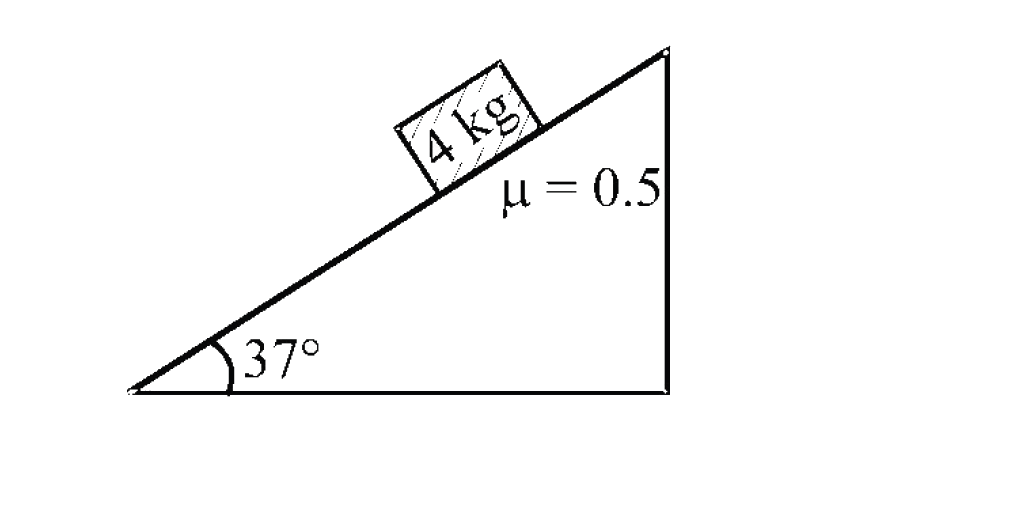
A 5-kg block rests on a smooth inclined plane of inclination 37∘ as shown in the diagram if the extension of spring is 6cm, find (a) the spring constant (b). If the block is pulled dow the incline 4 cm from its equilibrium position and released, find the initial acceleration of the block.
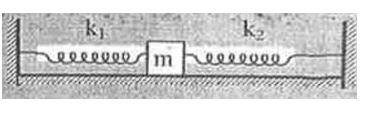
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

View Solution
Knowledge Check
For the system shown in figure, the acceleration of the block is :-
 A1m/s2B2m/s2C3m/s2D4m/s2
A1m/s2B2m/s2C3m/s2D4m/s2Two blocks (1 and 2) of equal mass m are connected by an ideal string (see figure shown) over a frictionless pulley. The blocks are attached to the ground by springs having spring constants k1 and k2 such that k1>k2
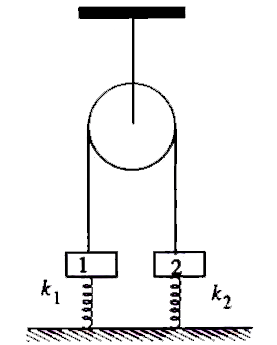
Initially, both springs are unstretched. The block 1 is slowly pulled down a distance x and released. Just after the release the possible values of the magnitude of the acceleration of the blocks a1 and a2 can be–AEither (a1=a2=(k1+k2)x2m) or (a1k1xm−ganda2=k2xm+g)B(a1=a2=(k1+k2)x2m) onlyC(a1=a2=(k1−k2)x2m) onlyD(a1=a2=(k1−k2)x2m) or (a1=a2=(k1k2)x(k1+k2)m−g)Two identical blocks A and B of mass m joined together with a massless spring as shown in figure are placed on a smooth surface. If the block A moves with an acceleration a0, then the acceleration of the block B is
 Aa0B−a0CFm−a0DFm
Aa0B−a0CFm−a0DFm
A block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
View SolutionA block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
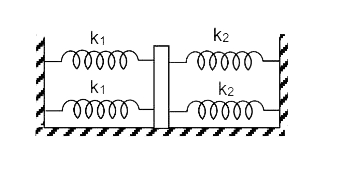
View SolutionTwo blocks each of the mass m are attached to the ends of a massless rod which pivots as shown in figure. Initially the rod is held in the horizontal position and then released. Calculate the initial angular acceleration.

View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

View Solution