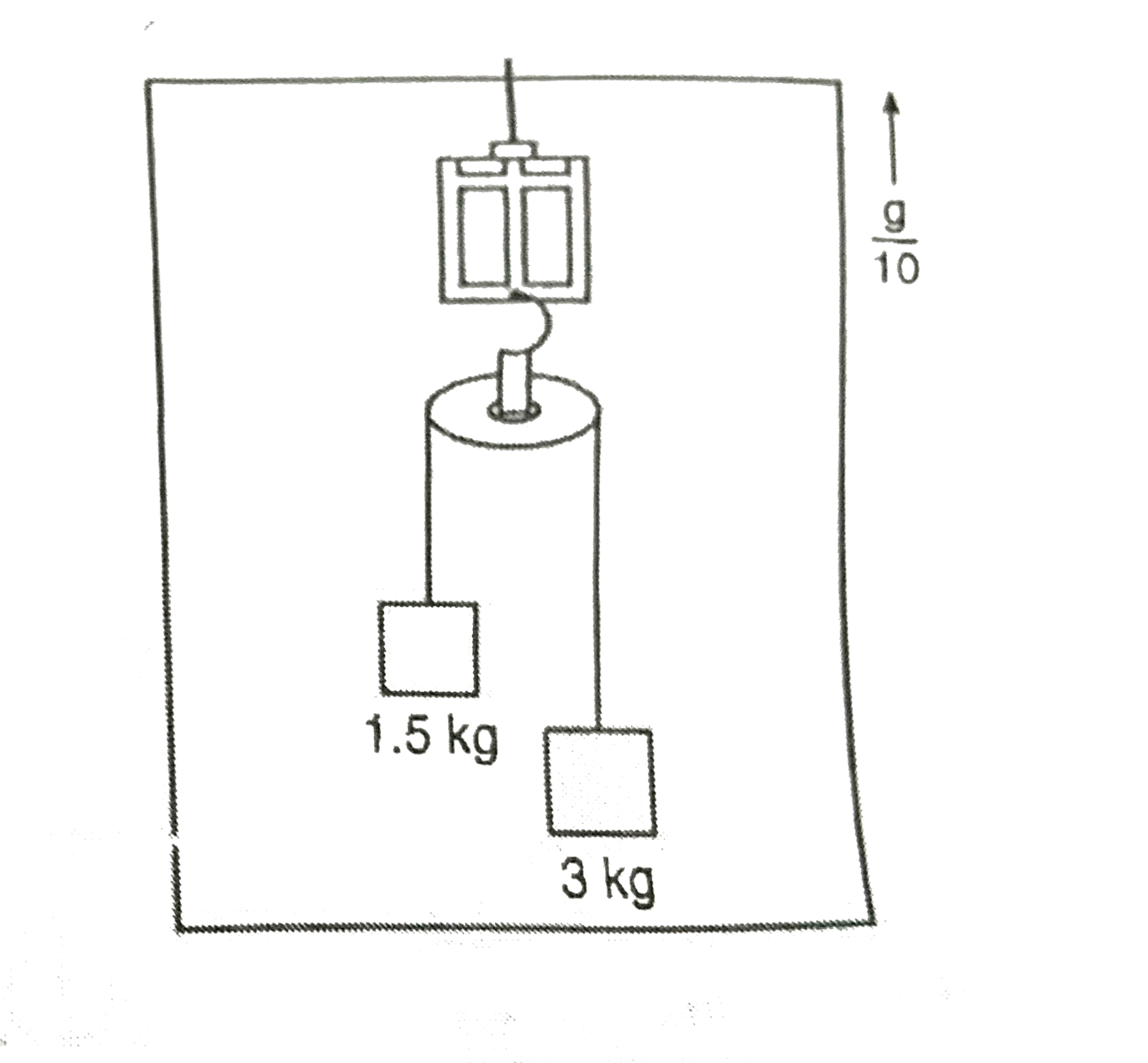
Find the reading of th spring balance shown in figure. The elevator is going up with an accelertion of g/10, the pulley and the strng are light and the pulley is smooth.

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of finding the reading of the spring balance when the elevator is accelerating upwards with an acceleration of $g / 10$ , we can follow these steps:
Step 1: Understand the Effective Gravity
When the elevator is accelerating upwards, the effective acceleration due to gravity increases. The effective gravitational force can be calculated as:
$g_{effective} = g + a$
where $a$ is the acceleration of the elevator. In this case, $a = \frac{g}{10}$ , so:
$g_{effective} = g + \frac{g}{10} = \frac{10 g}{10} + \frac{g}{10} = \frac{11 g}{10}$
Step 2: Set Up the Free Body Diagram
Consider two masses, $M_{1}$ (the heavier mass) and $M_{2}$ (the lighter mass). The tension in the string (T) acts upwards on both masses. For $M_{1}$ , the forces acting on it are:
- Weight downwards: $M_{1} g_{effective}$
- Tension upwards: $T$
For $M_{2}$ , the forces acting on it are:
- Tension upwards: $T$
- Weight downwards: $M_{2} g_{effective}$
Step 3: Write the Equations of Motion
Using Newton's second law, we can write the equations for both masses.
For $M_{1}$ :
$M_{1} g_{effective} - T = M_{1} a$
For $M_{2}$ :
$T - M_{2} g_{effective} = M_{2} a$
Step 4: Substitute $g_{effective}$ and Solve
Substituting $g_{effective} = \frac{11 g}{10}$ into the equations gives:
1. $M_{1} \frac{11 g}{10} - T = M_{1} a$
2. $T - M_{2} \frac{11 g}{10} = M_{2} a$
Step 5: Add the Two Equations
Adding the two equations to eliminate $T$ :
$M_{1} \frac{11 g}{10} - M_{2} \frac{11 g}{10} = M_{1} a + M_{2} a$
This simplifies to:
$(M_{1} - M_{2}) \frac{11 g}{10} = (M_{1} + M_{2}) a$
Step 6: Solve for Tension $T$
From the first equation, we can express $T$ :
$T = M_{1} \frac{11 g}{10} - M_{1} a$
Substituting $a = \frac{(M_{1} - M_{2}) \frac{11 g}{10}}{(M_{1} + M_{2})}$ into the equation for $T$ will yield the tension.
Step 7: Find the Spring Balance Reading
The reading of the spring balance is equal to $2 T$ (since there are two segments of the string pulling on the spring):
$Reading = 2 T$
Final Calculation
After substituting and simplifying, we find:
$T = \frac{4.4 g}{10}$
Thus, the reading of the spring balance will be:
$Reading = 2 T = 4.4 kg$
Conclusion
The reading of the spring balance is 4.4 kg.
---

Updated on:7/8/2024