A cylindrical bucket filled with water is whirled around in a vertical circle of radius r. What can be the minimum speed at the top of the path if water does not all out from the bucket ? If it continues with this speed, what normal contact force the bucket exerts on water at the lowest point of the path?

Video Solution

Text Solution

Verified by Experts

consider water as the system. At the top of the cfircle its acceleration towards the centre is vertically downward with magnitude $\frac{v^{2}}{r}$ . The forces on water asre ure.
a. weight Mg downward and
b. normal force by the bucket, aslso downward

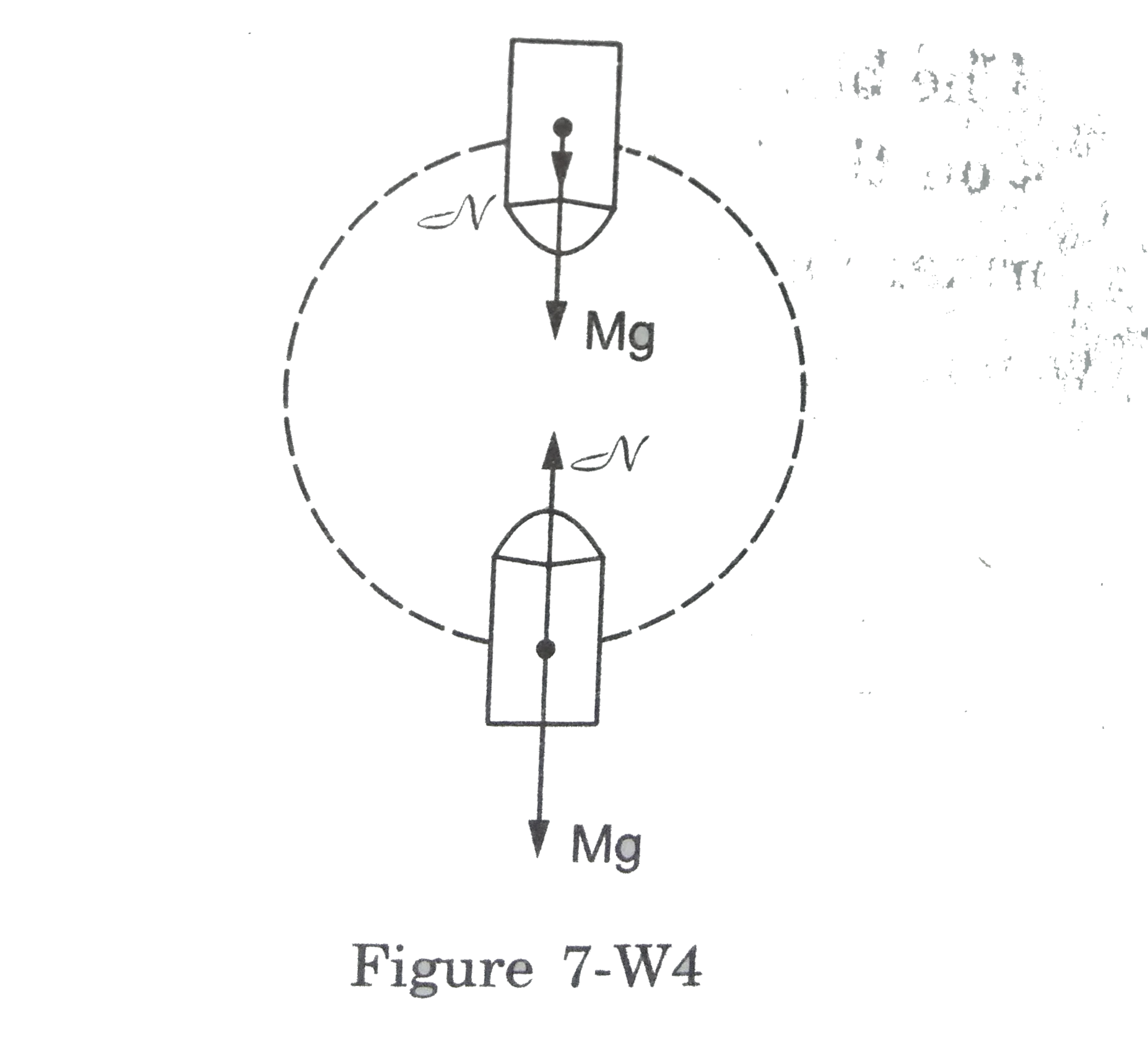
So, from Newton's second law
$M g = N = M \frac{v^{2}}{r}$
For water not to fall out from the bucket $N \geq 0$
Hence, $M \frac{v^{2}}{r} \geq M g or, v^{2} \to = r g$
the minimum speed at the top must be $\sqrt{r g}$
If the bucket continues on the circle with this minimum speed $\sqrt{r g}$ the forces at the bottom of theh path are
a. weight Mg downward and
b. normal contact force N by the bucket upward.
The acceleration is twoards the centre which is vertically upward, so
$N' - M g = M \frac{v^{2}}{g}$
$or, N' = M (g + \frac{v^{2}}{r}) = 2 M g$

Updated on:21/07/2023

A bucket full of water is revolved in vertical circle of radius 2 m . What should be the maximum time-period of revolution so that the water doesn't fall off the bucket
A $1 sec$
B $2 sec$
C $3 sec$
D $4 sec$
A bucket full of water is rapidly rotated in a vertical circle of radius r . It of is found that the water does not fall down from the bucket , even when the bucket is inverted at the highest point . If it continues with this speed , then the normal contact force exerted by the bucket on the water at the lowest point in its path is
Amg
B2mg
C $3 m g$
D $\frac{m g}{2}$
A bucket full of water is rotated in a vertical circle of radius R. If the water does not split out, the speed of the bucket at topmost point will be
A $\sqrt{R g}$
B $\sqrt{5 g R}$
C $\sqrt{2 R g}$
D $\sqrt{\frac{R}{g}}$