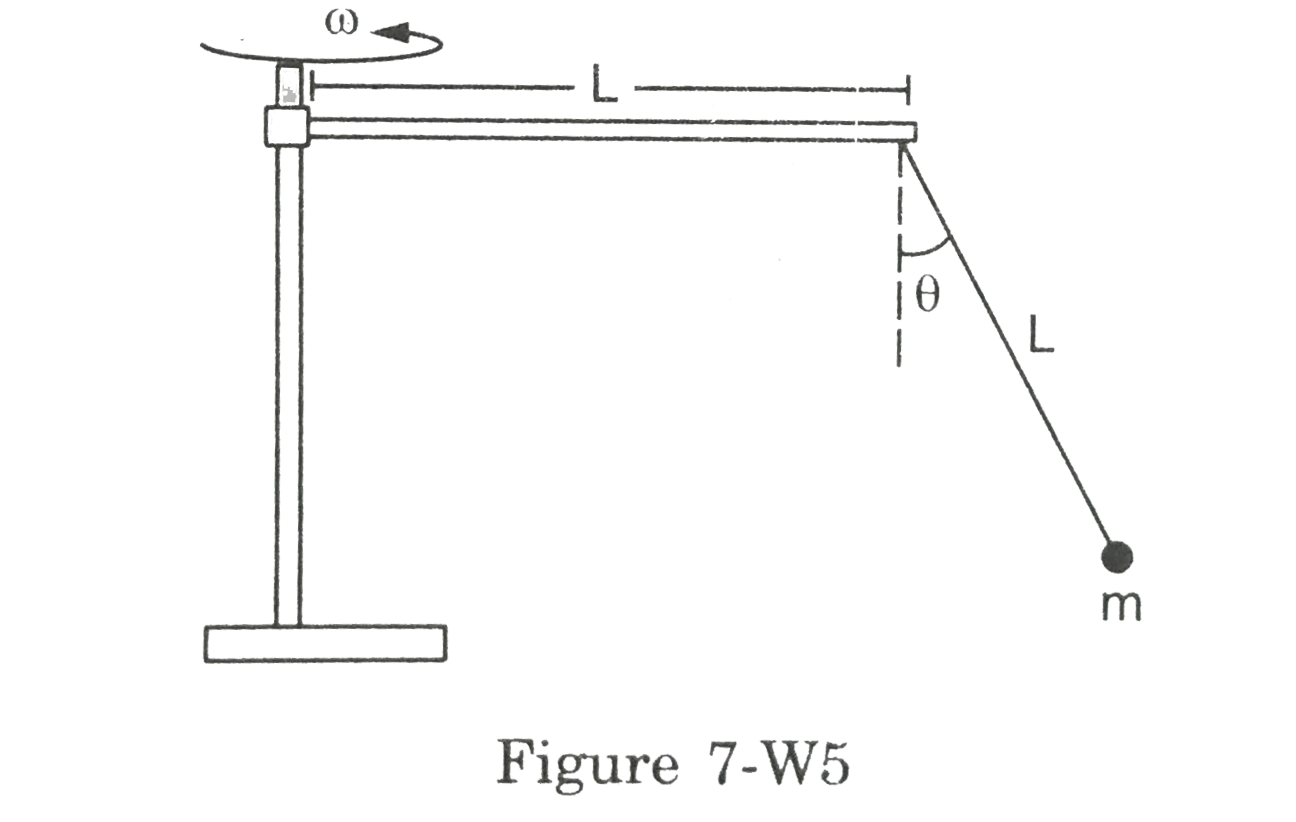
Figure shows as rod of length 20 cm pivoted near an end and which is made to rotate in a horizontal plane with a constant angular speed. A ball of mass m is spuspended by a string angular also of length 20 cm from the other end of the rod. If the angle $θ$ made by the stirng with the vertical is $30^{0}$ . find the anglular speed of the rotation. Take $g = 10 m / s^{2}$

$ω = 5.0 r a d / s$

$ω = 9.8 r a d / s$

$ω = 2.2 r a d / s$

$ω = 4.4 r a d / s$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
A stone tied to the end of a 20 cm long string is whriled in a horizontal ciecle with a constant angular speed .If the centripetal acceleration is $980 c m / s^{2}$ , its angular speed is .
A $7 r a d / s$
B $14 r a d / s$
C $π r a d / s$
D $20 r a d / s$
A pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed $ω$ such that the light inextensible string of length l of the pedulum makes a constant angle $θ$ with vertical. Find the
Q. angular speed $ω$

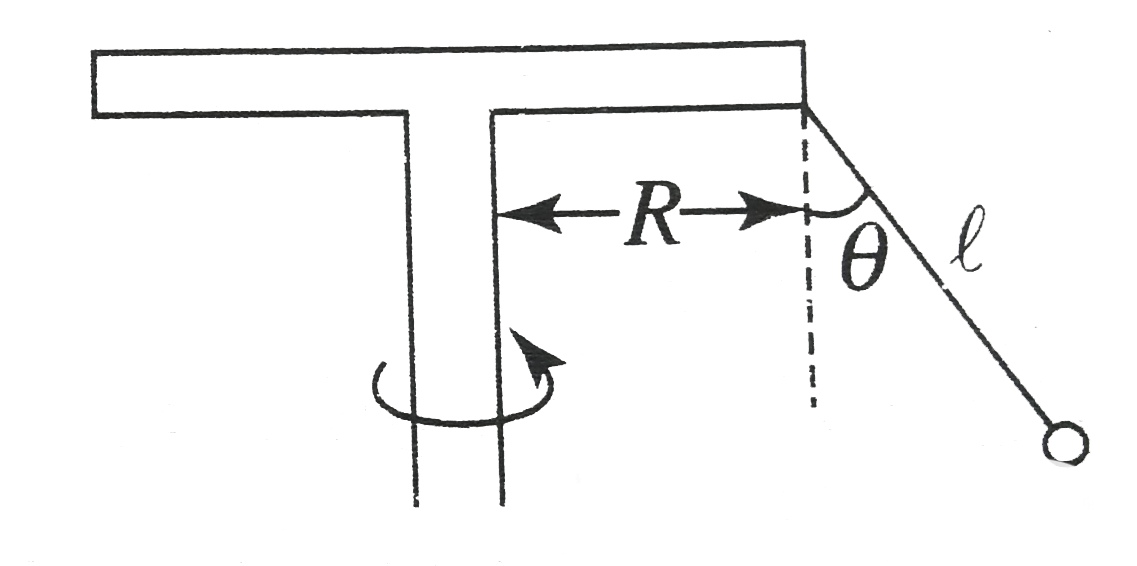A $ω = \sqrt{\frac{> a n θ}{R + l sin θ}}$
B $ω = \sqrt{\frac{> a n θ}{R + < a n θ}}$
C $ω = \sqrt{\frac{g cot θ}{R + l sin θ}}$
D $ω = \sqrt{\frac{> a n θ}{R + l cos θ}}$