A person stands on a spring balance at the equator. a.By wht fraction is the balance reading less than his true weight? b.If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the lenght o the day in this case?
The correct Answer is:A, B, C
To solve the problem step by step, we will break it down into two parts as given in the question.
Part A: Fractional Change in Balance Reading
1. Understanding True Weight and Balance Reading:
- The true weight W of a person is given by the gravitational force acting on them, which is W=mg, where m is the mass of the person and g is the acceleration due to gravity.
- The reading on the spring balance (normal force N) at the equator is affected by the centrifugal force due to the Earth's rotation.
2. Centrifugal Force:
- The centrifugal force Fc acting on the person can be expressed as:
Fc=m⋅R⋅ω2
where R is the radius of the Earth and ω is the angular velocity of the Earth.
3. Net Force on the Balance:
- The normal force (reading on the spring balance) is given by:
N=mg−Fc=mg−mRω2
- Thus, we can rewrite it as:
N=mg−mRω2
4. Fractional Change Calculation:
- The fractional change in the balance reading compared to the true weight is:
Fractional Change=W−NW=mg−(mg−mRω2)mg=mRω2mg
- Simplifying gives:
Fractional Change=Rω2g
5. Substituting Values:
- The angular velocity ω can be calculated as:
ω=2πT
where T=24×3600s (the time period of the Earth).
- Therefore, substituting ω:
Fractional Change=R(2πT)2g
- Substituting R=6400×103m and g=9.81m/s2:
Fractional Change=6400×103⋅(2π24×3600)29.81
6. Final Calculation:
- After calculating, we find that the fractional change is approximately:
Fractional Change≈3.5×10−3
Part B: Length of the Day for Half Weight Reading
1. Setting Up the Equation:
- If the reading on the balance is half the true weight, we have:
N=mg2
- Using the expression for N:
mg−mRω2=mg2
- Rearranging gives:
mRω2=mg2
2. Solving for Angular Velocity:
- Dividing by m and simplifying:
Rω2=g2
3. Substituting for ω:
- Using ω=2πT:
R(2πT)2=g2
- Rearranging gives:
T2=8π2Rg
4. Calculating the New Time Period:
- Substituting R=6400×103 and g=9.81:
T=√8π2(6400×103)9.81
5. Final Calculation:
- After calculating T, we find:
T≈7175.768s
- Converting to hours:
Length of the Day=7175.7683600≈1.993hours≈2hours
- The true weight W of a person is given by the gravitational force acting on them, which is W=mg, where m is the mass of the person and g is the acceleration due to gravity.
- The reading on the spring balance (normal force N) at the equator is affected by the centrifugal force due to the Earth's rotation.
- The centrifugal force Fc acting on the person can be expressed as:
Fc=m⋅R⋅ω2
where R is the radius of the Earth and ω is the angular velocity of the Earth.
- The normal force (reading on the spring balance) is given by:
N=mg−Fc=mg−mRω2
- Thus, we can rewrite it as:
N=mg−mRω2
- The fractional change in the balance reading compared to the true weight is:
Fractional Change=W−NW=mg−(mg−mRω2)mg=mRω2mg
- Simplifying gives:
Fractional Change=Rω2g
- The angular velocity ω can be calculated as:
ω=2πT
where T=24×3600s (the time period of the Earth).
- Therefore, substituting ω:
Fractional Change=R(2πT)2g
- Substituting R=6400×103m and g=9.81m/s2:
Fractional Change=6400×103⋅(2π24×3600)29.81
- After calculating, we find that the fractional change is approximately:
Fractional Change≈3.5×10−3
- If the reading on the balance is half the true weight, we have:
N=mg2
- Using the expression for N:
mg−mRω2=mg2
- Rearranging gives:
mRω2=mg2
- Dividing by m and simplifying:
Rω2=g2
- Using ω=2πT:
R(2πT)2=g2
- Rearranging gives:
T2=8π2Rg
- Substituting R=6400×103 and g=9.81:
T=√8π2(6400×103)9.81
- After calculating T, we find:
T≈7175.768s
- Converting to hours:
Length of the Day=7175.7683600≈1.993hours≈2hours
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective 2
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
Similar Questions
A person stands on a spring balance at the equator.
(a) How much is the reduction in weight as measured by the balance.
(b) If the speed of earth's rotation is changed such that the balance reading is half of its true weight, what will be the length of the day in this case? (g=10m/s2,Re=6400km)
View SolutionA body hangs from a spring balance supported from the ceiling of an elevator.
(a) If the elevator has an upward acceleration of 2.45m/s2 and the balance reads 50 N, what is the true weight of the body?
(b) Under what circumstances will the balance read 30 N?
(c) What will be the reading in the balance if the cable of the elevator breaks ?
View Solution
Knowledge Check
The angular velocity of the earth's rotation about its axis is ω. An object weighed by a spring balance gives the same reading at the equator as at height h above the poles. The value of h will be
Aω2R2gBω2R22gC2ω2R2gD2ω2R23gA body is suspended on a spring balance in a ship sailing along the equator with a speed v'. If ω is the angular speed of the earth and ω0 is the scale reading when the ship is at rest, the scale reading when the ship is sailing is
Aw0BzeroCW0(1±2wvg)DW0(1−g2w)A person holds a spring balance with a mass m hanging from it goes up and up in a helicopter, then reading of weight of body as indicated by spring balance will.
Abe increasingBbe decreasingCfirst increase and then decreaseDremain the same.
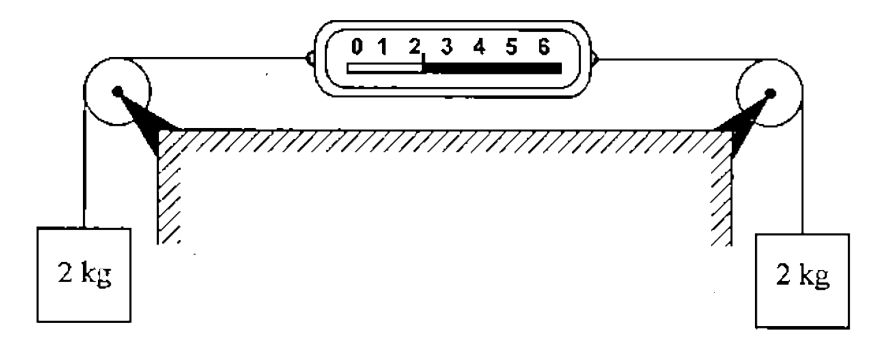
Two 2 kg weight are attached to spring balance as shown in figure-2.122. What is the reading of the scale ?
View SolutionA body hangs from a spring balance supported from the roof of an elevator.
(a) If the elevator has an upward acceleration of 2.45ms−2 and the balance reads 50N, what is the true weight of the body?
(b) Under what circumstances will the balance read 30N?
(c) What will be the balance reading if the elevator, cable breaks?
View SolutionA body is weighed on a spring balance in the wagon of a train travelling round a bend in the track which is banked in the usual way. The balance shows increase in weight by fraction n. The balance can revolve about its support point and remains at right angles to the floor of the wagon when rounding the bend when the train is travelling at speed v ?
View SolutionThe angular speed of rotation of earth about its axis at which the weight of man standing on the equator becomes half of his weight at the poles is given by
View SolutionA body is suspended on a spring balance in a ship sailing along the equator with a speed v'. If ω is the angular speed of the earth and ω0 is the scale reading when the ship is at rest, the scale reading when the ship is sailing is
View Solution