What is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle $θ$ with the horizontal, at a point where the velocity of particle makes an angle $θ / 2$ with the horizontal.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

Let v the velocity at the point where it makes an angle $\frac{θ}{}$ with horizontal.
The horizontal component remains unchanged.
So, $v cos (\frac{θ}{2}) = u cos θ$

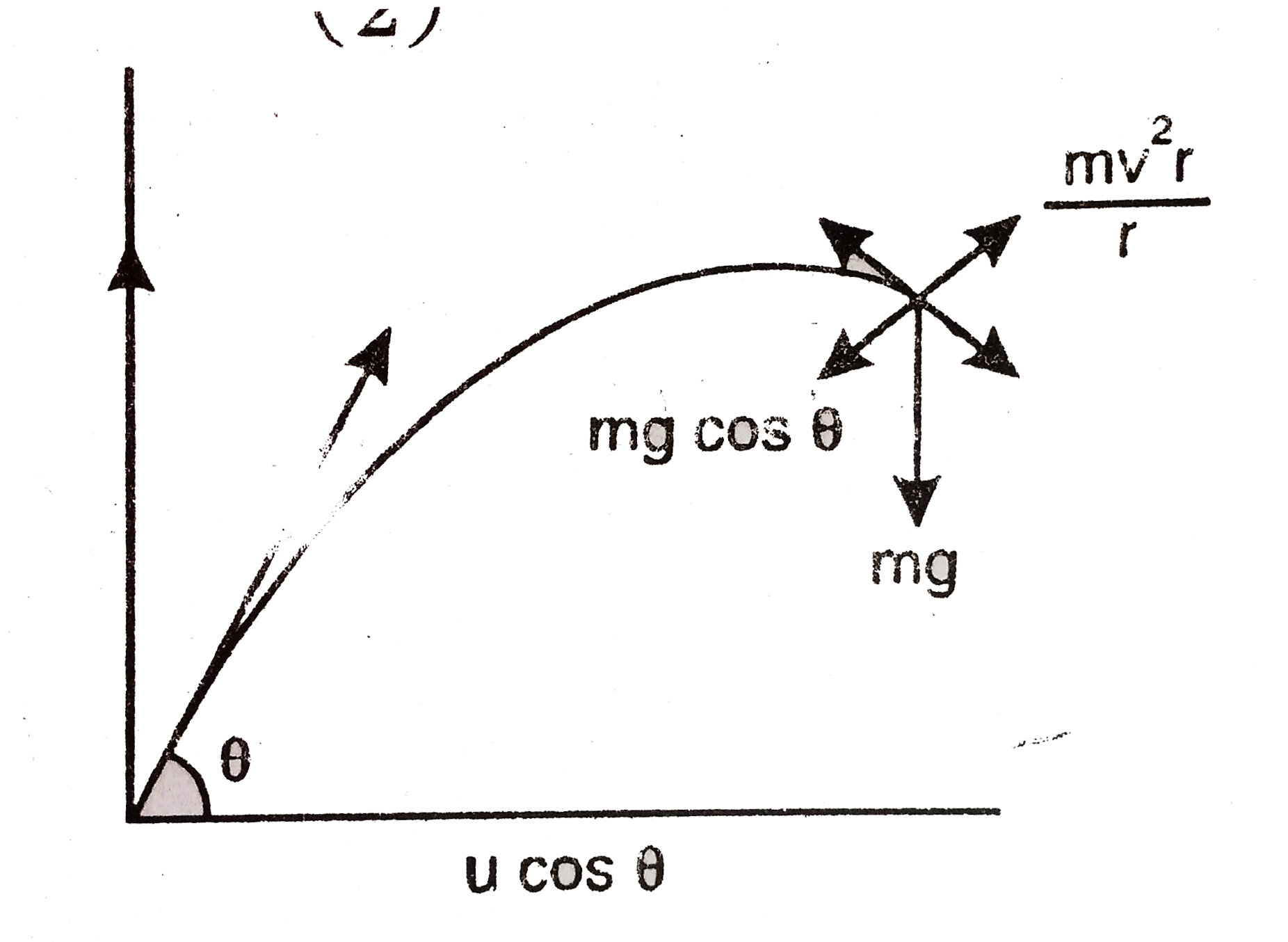
$\to v = \frac{u cos θ}{cos (\frac{θ}{2})}$ …….i
From ure, $m g cos (\frac{θ}{2}) = \frac{m v^{2}}{r}$
$\to r = \frac{v^{2}}{g cos (\frac{θ}{2})}$
putting the value of v from equation i.
$r = \frac{v^{2} {cos}^{2} θ}{g {cos}^{2} (\frac{θ}{2})}$

|

Updated on:21/07/2023

Class 11 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A projectile is projected with a speed $u$ at an angle $θ$ with the horizontal. What is the speed when its direction of motion makes an angle $θ / 2$ with the horizontal
A $\frac{u cos θ}{2}$
B $u cos θ$
C $u (2 \frac{cos (θ)}{2} - \frac{sec (θ)}{2})$
D $u (\frac{cos (θ)}{2} - \frac{sec (θ)}{2})$
Question 2 - Select One
A particle is projected with a speed u at an angle $θ$ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle $α$ with the horizontal?
A $u cos θ sec α$
B $u sec θ cos α$
C $u cos θ tan α$
D $u cos θ cot α$
Question 3 - Select One
A particle is thrown with a speed u at an angle $θ$ with the horizontal. When the particle makes an angle $ϕ$ with the horizontal. Its speed changes to v :
A $v = u cos θ$
B $v = u cos θ . cos ϕ$
C $v = u cos θ . sec ϕ$
D $v = u sec θ . cos ϕ$

HC VERMA-CIRCULAR MOTION-Exercises

Home
Ask Doubt
Profile