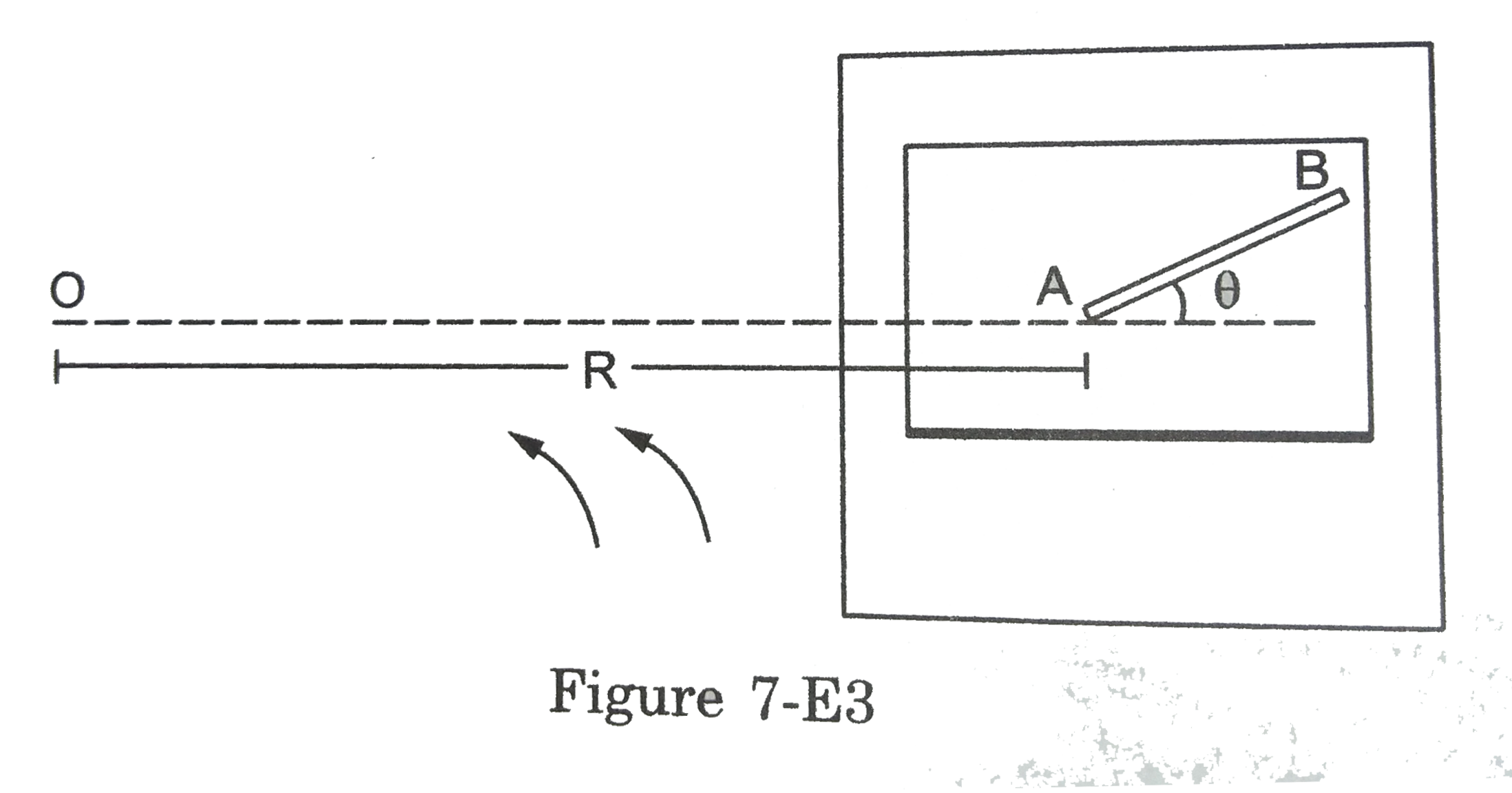
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular pathof radius R. A smooth groove AB of length L(<<R) is made on the surface of the table. The groove makes an angleθ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by tehparticle to reach the point B.
The correct Answer is:A, B, C
The cabin rotates with angular velocity ωs and radius R.
∴ The particle experiences a force mRω2.
The component of mRω2 alogn the provided force to the particle to move along AB.
∴mRω2cosθ=ma
→a=Rω2cosθ
Length of groove L<br>L=ut+12at2
→L=12Rω2cosθt2
→t2=2LRω2cosθ
→t=√2LRω2−cosθ
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective 2
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
Similar Questions
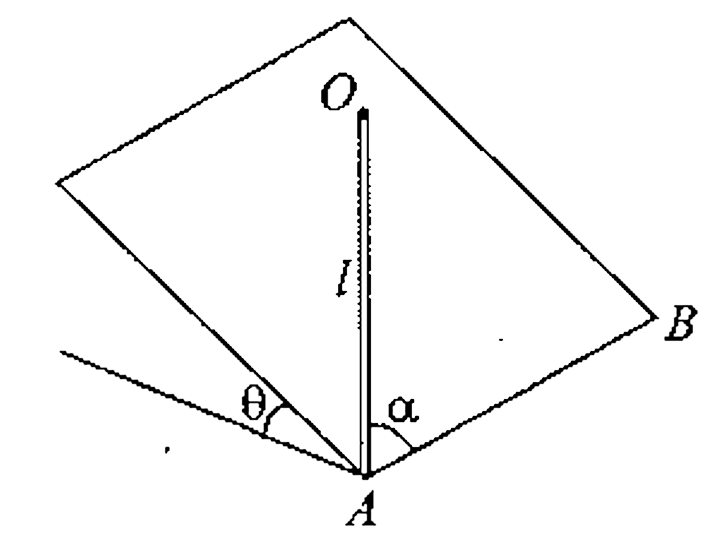
There is an inclined surface of inclination θ. A smooth groove is cut into it forming an angle α with AB as shown in figure. A steel ball is free to slide a long the groove. If the ball is released from the point O. Find the speed when it comes to A.
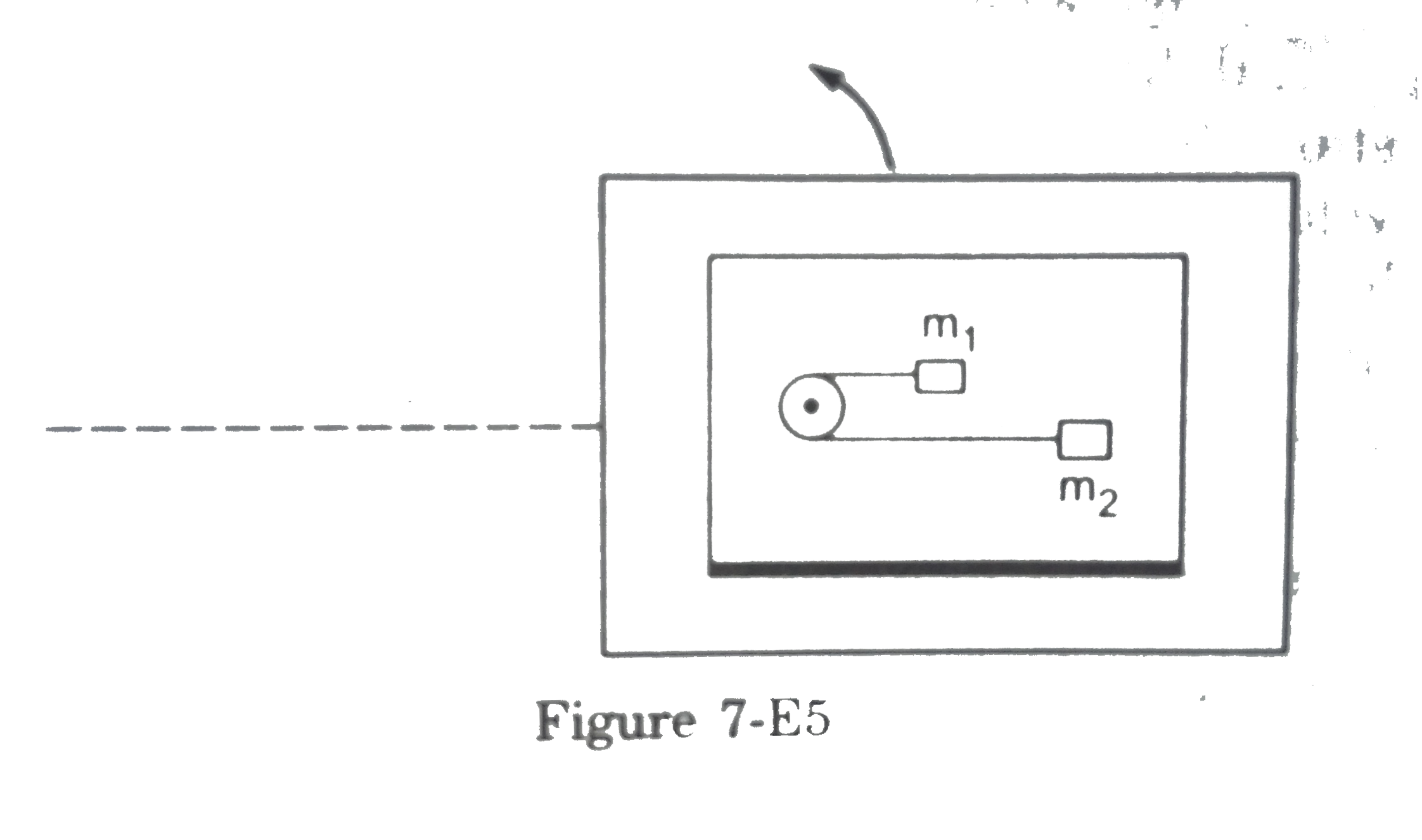
View SolutionA table with smooth horizontal surface is placed in a cabin which moves in a circle of a large radius R Figure. A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on te tableare connected through a string going over the pulley. Initially the masses are held by a personwith the strings aslong teh outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the mases as seen from the cabin and the tension in the starting.
View Solution
Knowledge Check
A table with smooth horiztonal surface is truning at an angular speed ω abouyt its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
Av=ω2(L2−a2)13Bv=ω(L2−a2)Cv=ω2√L2−a2Dv=ω√L2−a2A uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
Aml2ωBml2ω3Cml2ω12Dml2ω6A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
A table with smooth horizontal surface is placed in a cabin which moves in a circle of a large radius R = 100 m with ω = 3 rad/s (see figure ) . A smooth pulley of small radius is fastened to the table . Two masses m and 2m placed on the table are connected through a string going over the pulley . initially the masses are held by a person with the strings along the outward radius and then the system is released from rest (with respect to the cabin ) . Then the magnitude of the initial acceleration of the mass m as seen from the cabins is n×100. Find n .

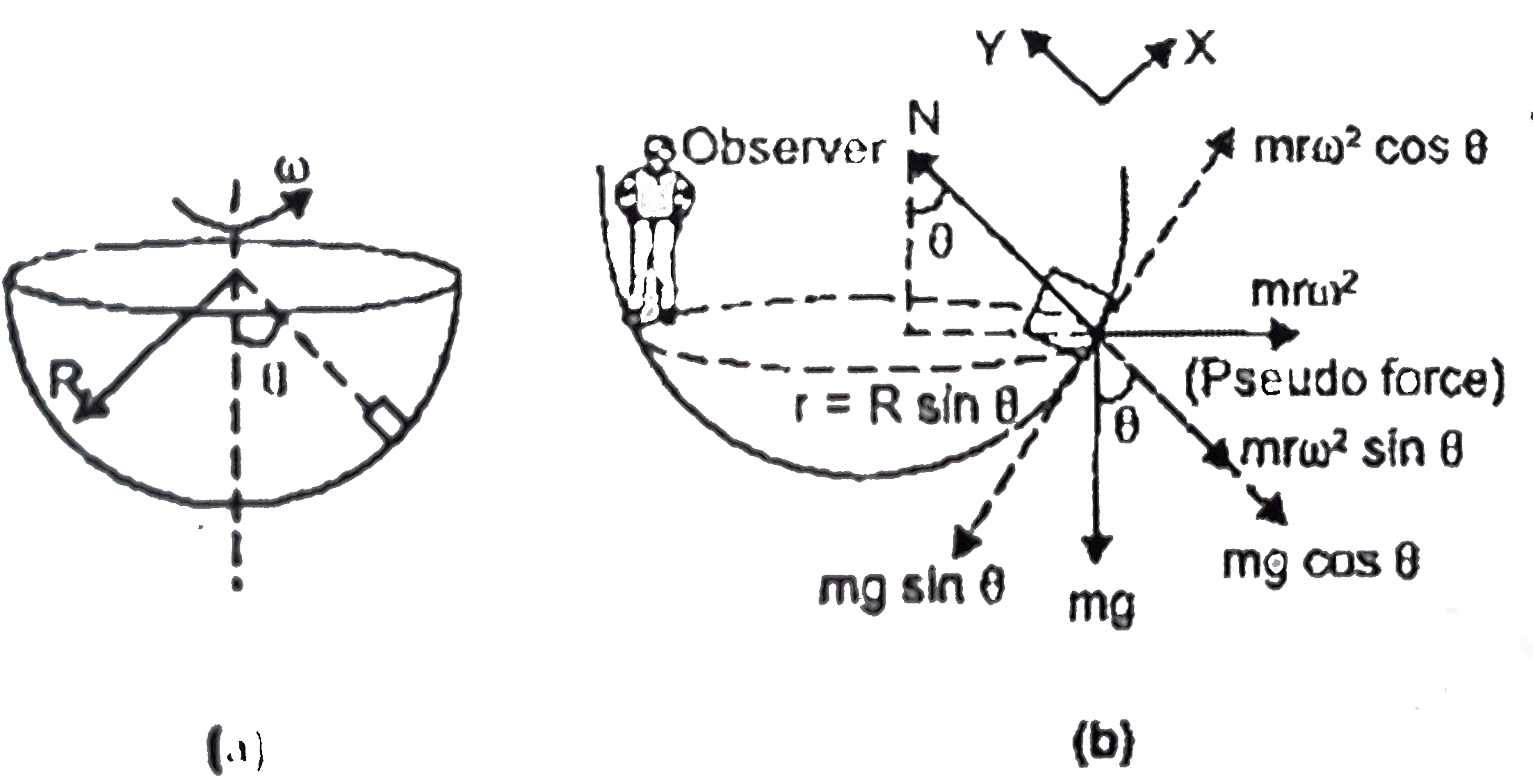
View SolutionA block is kept inside a hemispherical bowl rotating with angular velocity ω. Inner surface of bowl is rough, coefficient of friction is μ. The block is kept at a position where radius makes an angle θ with the vertical. What is the range of the angular speed for which the block will stay at the given position?
View SolutionA smooth horizontal disc rotates about the vertical axis O (figure) with a constant angular velocity ω. A thin uniform rod AB of length l performs small oscillation about the vertical axis A fixed to the disc at a distance a from the axis of the disc. Find the frequency ω0 of these oscillations.

View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionA horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -

View Solution