A bullet of mass 10 g moving horizontally at asped dof strikes a block of mass 490 g kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular tract o radius 0.2 m. Where will the block strike the horizontal part after leaving the semicircular track?

mass of block =490 gm
mss of bullet = 10gm
Since the bullet embedded inside the block, it is a plastic collision
Initial velocity of bullet
velocity of the block is
Let fiN/Al velocity of boty =v
Hence
ltbr> When the block loses the contat at D the component mg will act on it,
.........i
puting work energy principle
rarr 3.5-0.98sinthea=1.96+1.96sinthetararr sintheta=(1/2)rarr theta=30^0:. Angle of projection
time of reaching the ground
,
S=vcos q xxt=sqrt(grsintheta) cos thetaxxt =sqrt(9.8xx2xx(1/2)sqrt3/2xx0.2470.196m=(0.2-0.2cos30^0+0.196)=0.22m
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective 2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
A bullet of mass 10kg moving horizontally at a speed 140m/s strikes a block of mass 100g attached to a string like a simple pendulum. The bullet penetrates the block and emerges on the other side. If the block rises by 80cm , find final velocity of bullet.
View SolutionA bullet of mass 10 g moving with a speed of 20m/s hits an ice block of mass 990 g kept on a frictionless floor and gets stuck in it. How much ice will melt if 50% of the lost kinetic energy goes to ice?
(Temperature of ice block =0∘C.)
View Solution
Knowledge Check
A bullet of mass 10g moving horizontally with a speed of 400m/s a block of mass 390g and remains in it. The block slides 10m on rough surface before coming to rest. The friction coefficient is
A14B12C34D1A bullet of mass 10 g moving with 300m/s hits a block of ice of mass 5 kg and drops dead. The velocity of ice is
A50cm/sB60cm/sC40cm/sD200cm/sA bullet of mass 20g moving horizontally strikes a block of mass 480g suspended by a string of length 2m. If the collision is completely inelastic , the minimum velocity of bullet , so that the combined mass complete vertical circle should be
A100m/sB150m/sC200m/sD250m/s
A bullet of mass 10 g moving with a speed of 20m/s hits an ice block of mass 990 g kept on a frictionless floor and gets stuck in it. How much ice will melt if 50% of the lost kinetic energy goes to ice?
(Temperature of ice block =0∘C.)
View SolutionA bullet of mass 10 g travelling horizontally with a velocity of 300 m/s strikes a block of wood of mass 290 g which rests on a rough horizontal floor. After impact the block and the bullet move together and come to rest when the block has travelled a distance of 15 m. The coefficient of friction between the block and the floor will be - (Duration of impact is very short)
View SolutionA bullet of mass 0.01 kg travelling at a speed of 500 m/s strikes a block of mass 2 kg, which is suspended by a string of length 5 m. The centre of gravity of the block is found to rise a vertical distance of 0.1 m. The speed of the bullet after it emerges from the block will be -
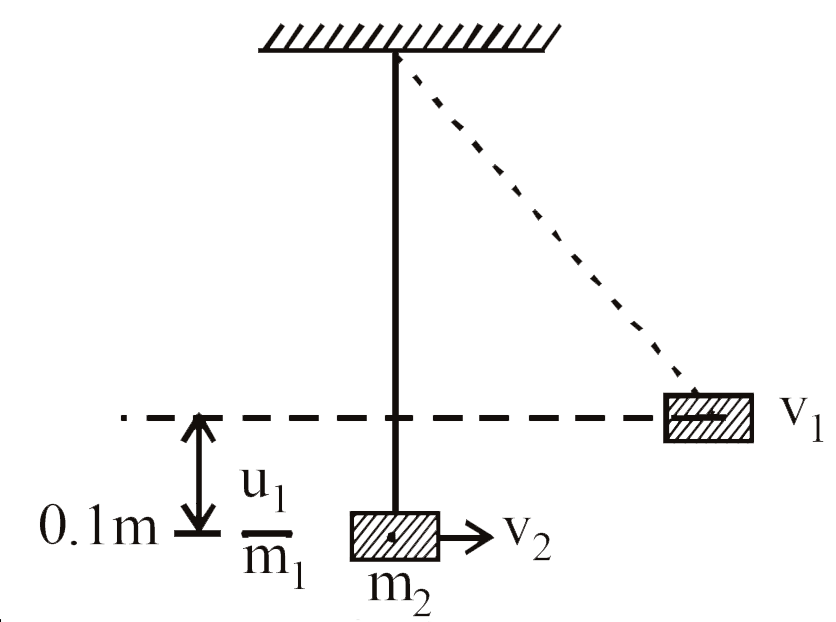
View SolutionA bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
View SolutionA bullet of mass 10 g moving horizontally with a velocity of 400ms−1 strikes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5 m. As a result, the centre of gravity of the block is found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges out horizontally from the block will be
View Solution
