A bucket is being lowered down into a well through a rope passing over a fixed pulley of radius 10 cm. Assume that the rope does not slip on the pulley. Find the angular velocity and angular acceleration of the pulley at an instant when the bucket is going down at at speed of 20 cm/s adn has an accelertion of 4.0ms2.
Since the rope does not slip on the pulley, the linear speed v of therim of the pulley is same as the speed of the bucket.
the anguklar velocity of the pulley is then
ω=vr=20cms10cm=2rads
and the angular acceleration of the pulley is
αar4.0ms210cm=40rads2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Worked Out Examples
29 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Short Answer
22 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A particle is moving in a circle of radius 0.3 . Calculate its linear acceleration at the instant when its angular velocity is 1rad/s and angular acceleration is 4rad/s2
View SolutionCalculate the linear acceleration of a particle of a particle moving in a circle of radius 0.4 m at the instant when its angular velocity is 2 rad s−1 and its angular acceleration is 5 rad s−2.
View Solution
Knowledge Check
A particle moves in a circle of radius 20 cm with linear speed of 10 m/s. Find the angular velocity
A500radsB150radsC50radsD15radsA belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of 5m/s, the belt is moving with an angular velocity of
A3.2rad/sB0.32rad/sC20rad/sD0.032rad/sA particle moves along a circle of radius 10 cm . If its linear speed changes from 4m/s to 5 m/s in 1 s, then its angular acceleration will be
A2 rad /s2B5 rad /s2C10 rad /s2D8 rad /s2
Calculate the magnitude of linear acceleration of a particle moving in a circle of radius 0.5 m at the instant when its angular velocity is 2.5 rad s–1 and its angular acceleration is 6rads−2.
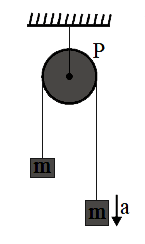
View SolutionIn the figure, the blocks unequal masses m1 and m2 (m1<m2).m2 has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
View SolutionCalculate the magnitude of linear acceleration of a particle moving in a circle of radius 0.5m at the instant when its angular velocity is 25rads−1 and its angular acceleration is 6rads−2.
View SolutionA belt moves over two pulleys A and B as shown in the figure. The pulleys are mounted on two fixed horizontal axles. Radii of the pulleys A and B are 50 cm and 80 cm respectively. Pulley A is driven at constant angular acceleration of 0.8 rad/s2 unitl pulley B acquries an angular velocity of 10 rad/s. The belt does not slide on either of the pulleys.
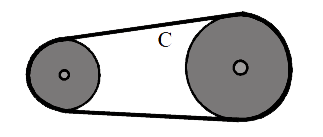
(a)Find the acceleration of a point C on the belt and angular acceleration of the pulley B.
(b) How long does it take for the pulley B to acquire an angular velocity of 10 rad/s ?
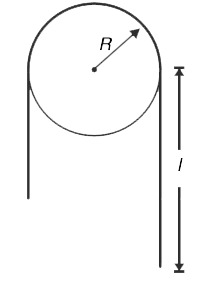
View SolutionA rope of length L and mass per unit length λ passes over a disc shaped pulley of mass M and radius R. The rope hangs on both sides of the pulley and the length of larger hanging part is l. The pulley can rotate about a horizontal axis passing through its centre. The system is released from rest and it begins to move. The pulley has no friction at its axle and the rope has large enough friction to prevent it from slipping on the pulley.
(a) Find the acceleration of the rope immediately after it is released.
(b) Find the horizontal component of the force applied by the axle on the pulley immediately after the system is released
View Solution
