A rectangular plate of sides a and b is suspended fropm a ceilling by two parallel strings of length L each figure. The separation between the strings is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute harmonic motion. Find the time period.

The correct Answer is:B
Here we have to consider oscillation of centre of mass.
Driving force, F=mg sin theta<br>Ae≤ration=a=sm=gsinθ
∴A=>hη=g(mL)
[wehre g and L and const].
∴Aαx
So the motion is simple Harmonic.
Timeperiodt=2pisqrt(displacement/Acceleration)<br>=2pi sqrt(x/(gx/L))=2pi sqrt(L/g)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A rectangular plate of mass M, sides l1 and l2 is suspended from a ceiling by two parallel strings of length l3 each as shown in figure. The plate is displaced slightly in its plane keeping the strings tight. The angular frequency of its SHM is ω. Find the value of 2ω2 in SI units. [Take: M=10kg,l1=0.8m,l2=0.2m,l3=0.4m].
'(##CEN_KSR_PHY_JEE_C16_E01_037_Q20##)'
View SolutionConsider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
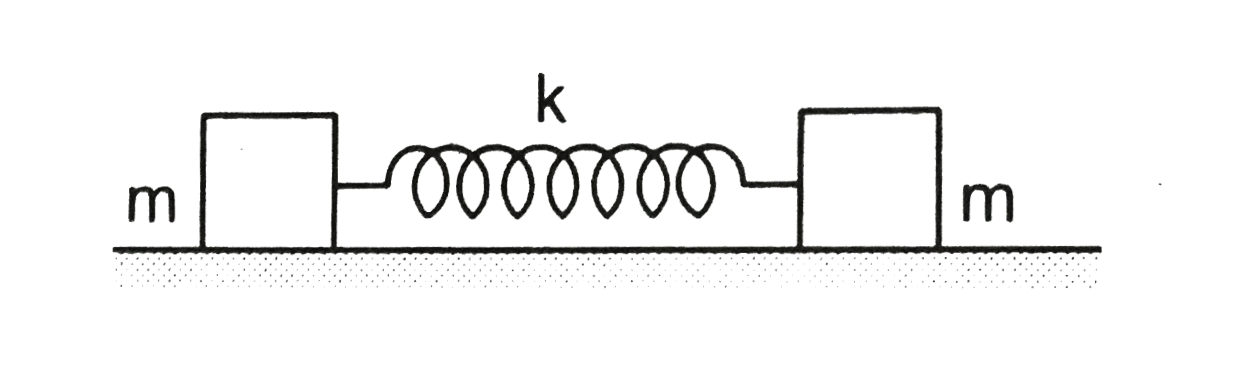
View Solution
Knowledge Check
A particle of mass m is suspended from a fixed O by a string of length L. At t=0, it is displaced from its equilibrium position and released. The graph which shows the variation of the tension T in the string with time t is :
 A
A B
B C
C D
D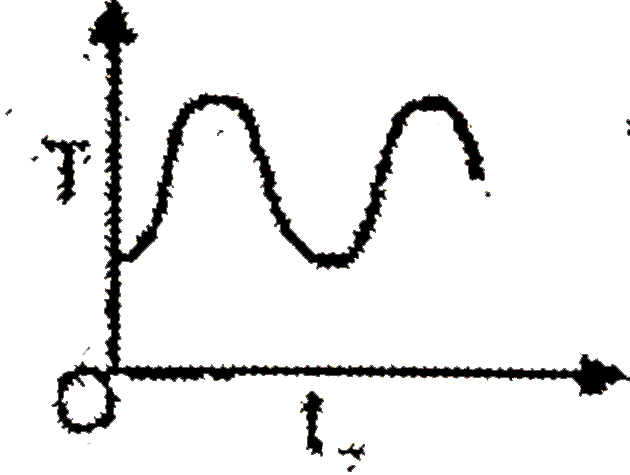
A thin uniform square plate ABCD of side a and mass m is suspended in a vertical plane as shown in the figure. AE and BF are two massless inextensible strings. The line AB is horizontal. The tension in AE just after BF is cut will be
 A2mg5BmgC2mg7D3mg5
A2mg5BmgC2mg7D3mg5Six plates each of area A arranged as shown· in figure. The separation between adjoining plates is d. Find the equivalent capacitance between points A and B :
 Aε0AdB7ε0AdC6ε0AdD5ε0Ad
Aε0AdB7ε0AdC6ε0AdD5ε0Ad
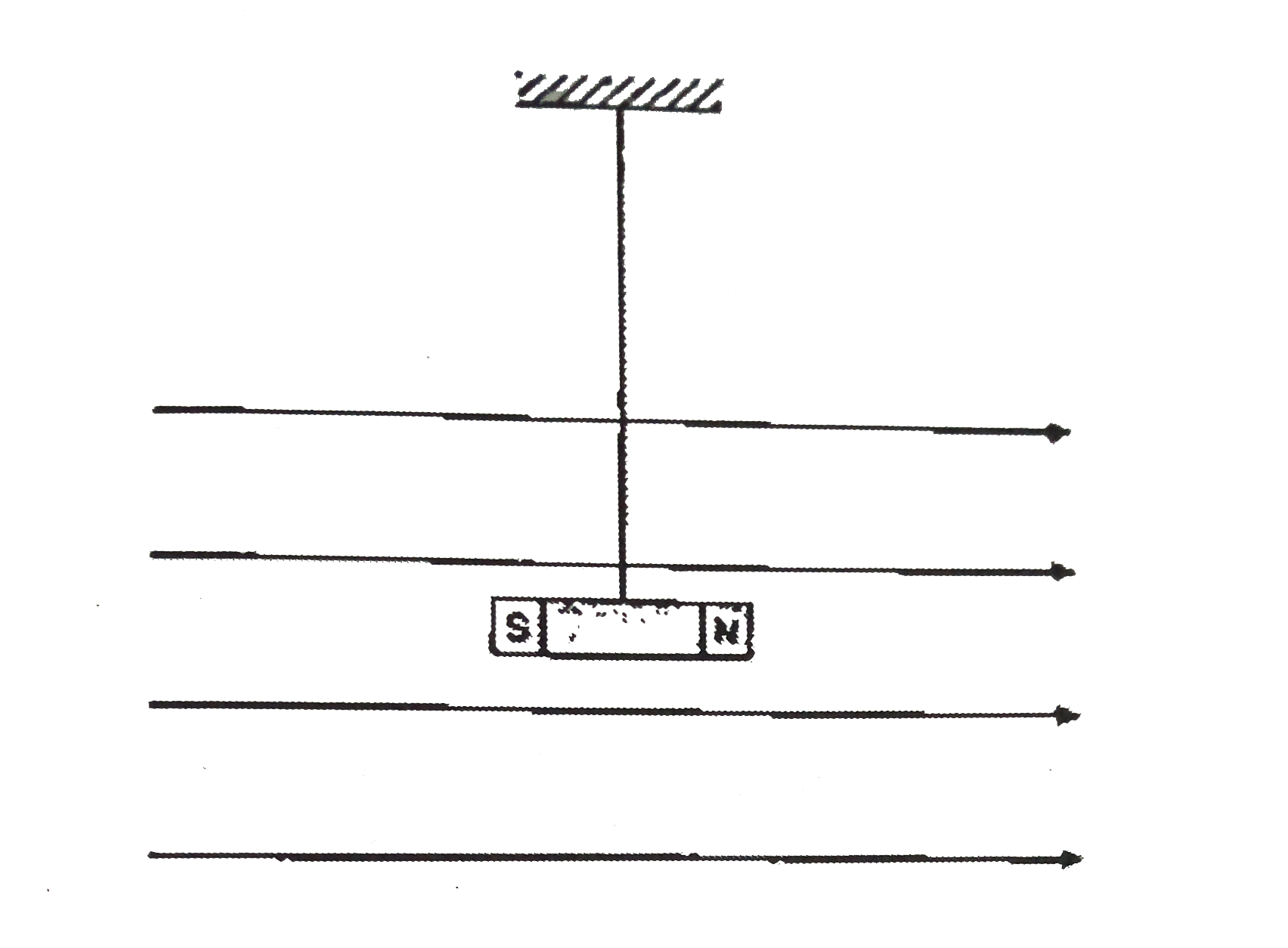
A magnetic dipole of magnetic moment M is suspended by a string in a uniform horizontal magnetic field as showo in figure. If in horizontal plane this dipole is slightly tilted and released, show that it will execute simple harmonic motion and find its oscillation period. Consider the dipole as a uniform rod of mass m and length I.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
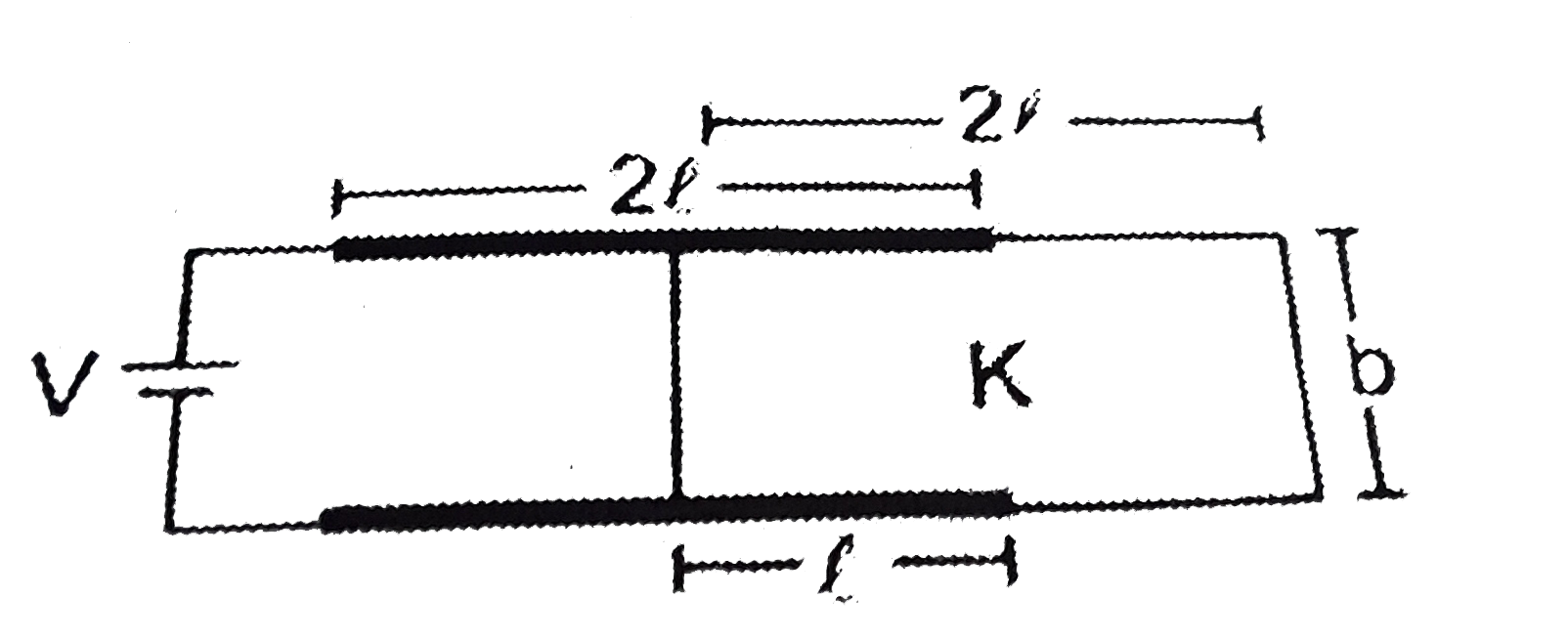
View SolutionThe plates of the parallel plate capacitor have plate area A and are clamped in the laboratory as shown in figure. The dielectric slab of mass m, length 2l and width 2l is released from rest with length l inside the capacitor. Neglecting any effect of friction or gravity, show that the slab will execute periodic motion and find its time period. (plates of capacitor are square plates of side 2l)
View SolutionTwo identical pith balls are charged by rubbing against each other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. in equilibrium, the separation between the balls in 3 cm. Find the mass of each ball and the tension in the strings. the charge on each ball a magnitude 2.0×10−8C.
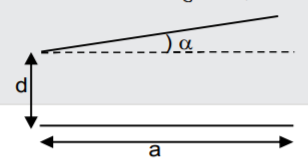
View SolutionTwo square plates of side 'a' are arranged as shown in the figure. The minimum separation between plates is 'd' and one of the plate is inclined at small angle α with plane parallel to another plate. The capacitance of capacitor is (given α is very small)
View Solution