In a quadrilateral ABCD, P and Q are mid-ponts. Show that ar(AXD)+ar(BYC)=ar(PXQY)
Step by step video solution for In a quadrilateral ABCD, P and Q are mid-ponts. Show that ar(AXD)+ar(BYC)=ar(PXQY) by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023समान प्रश्न
ज्ञान जांच
In a ∣∣gm ABCD, if P and Q are midpoints of AB and CD respectively and ar(||^(gm) ABCD) =16cm2 then ar (∣∣gm APQD) = ?
 A8cm2B12cm2C6cm2D9cm2
A8cm2B12cm2C6cm2D9cm2
In a quadrilateral ABCD, it is being given that M is the midpoint of AC. Prove that
ar(□ABMD)=ar(□DMBC).

View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
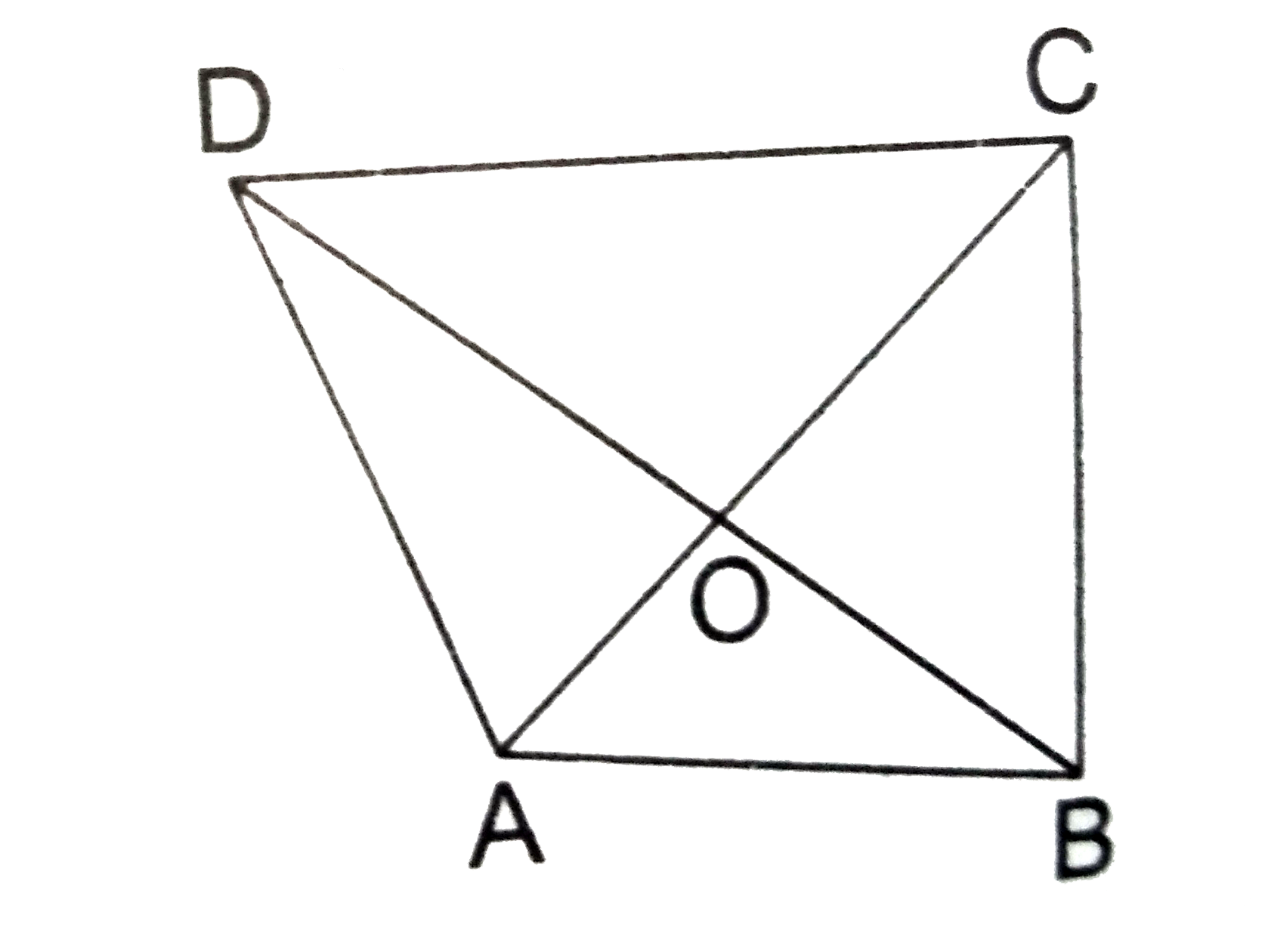
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
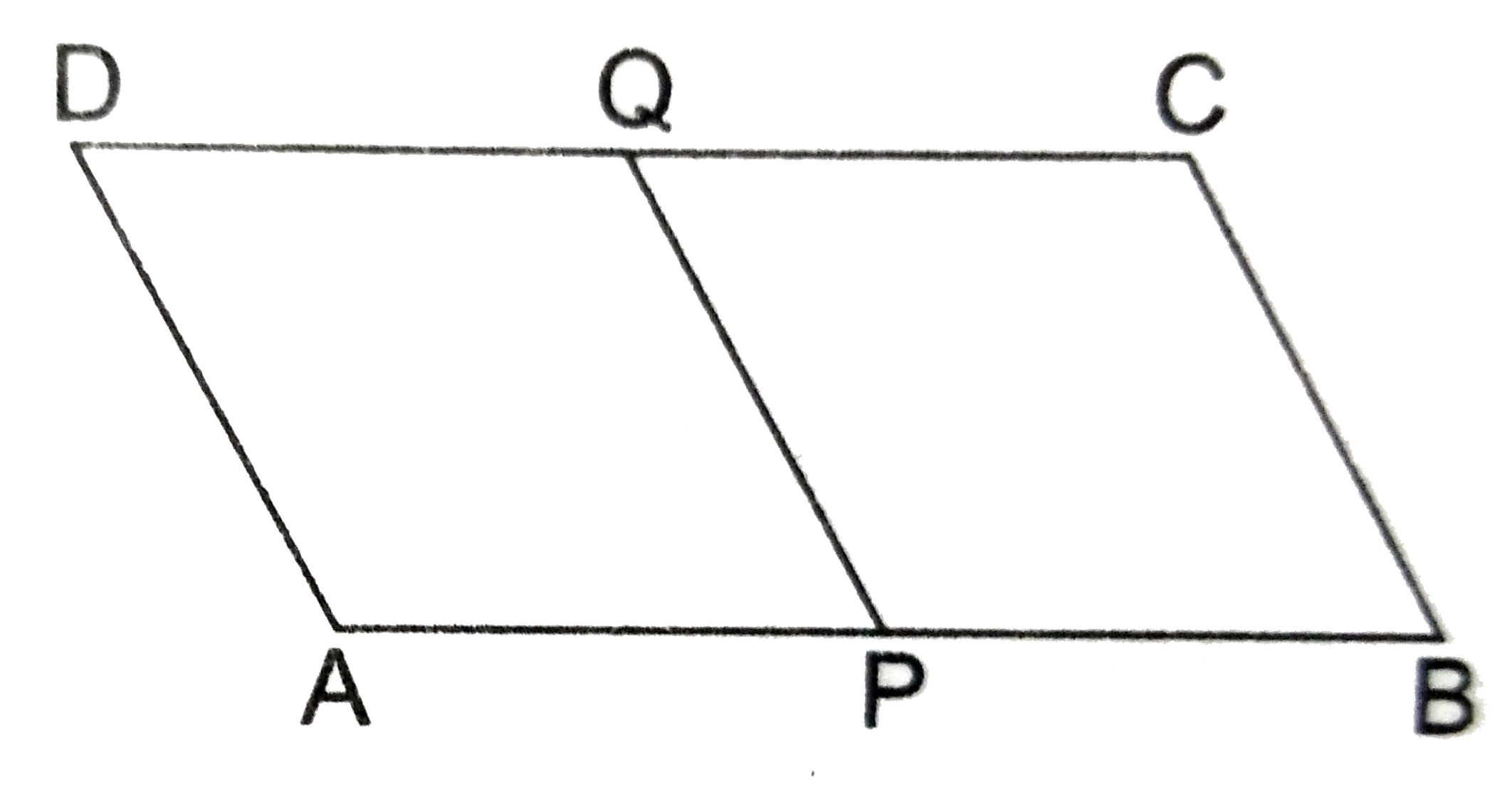
View SolutionIn trapezium ABCD, AB∣∣DC and L is the mid-point of BC. Through L, a line PQ∣∣AD has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

View SolutionIn trapezium ABCD, AB∣∣DC and L is the mid-point of BC. Through L, a line PQ∣∣AD has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

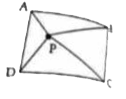
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
View Solution
