In trapezium ABCD, AB∣∣DC and L is the mid-point of BC. Through L, a line PQ∣∣AD has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

Given In trapezium ABCD, AB∣∣DC, DC produced in Q and L is the mid-point of BC.
∴ BL = CL
To prove ar(ABCD)=ar(APQD)
Proof Since, DC produced in Q and AB∣∣DC.
So, DQ∣∣AB
In ΔCLQ and ΔBLP,
CL=BL [since, L is the mid-point of BC]
∠LCQ=∠LBP [alternate interior angles as BC is a transversal]
∠CQL=∠LPB [alternate interior angles as PQ is a transversal]
∴ ΔCLQ≅ΔBLP [by AAS congruence rule]
Then, ar(ΔCLQ)=ar(ΔBLP) ...(i)
[since, congruent triangles have equal area]
Now, ar(ABCD)=ar(APQD)−ar(ΔCQL)+ar(ΔBLP)
=ar(APQD)−ar(ΔBLP)+ar(ΔBLP) [from Eq. (i)]
⇒ ar(ABCD)=ar(APQD) Hence proved.
Topper's Solved these Questions
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.2 Very Short Answer Type Questions
5 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
Similar Questions
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
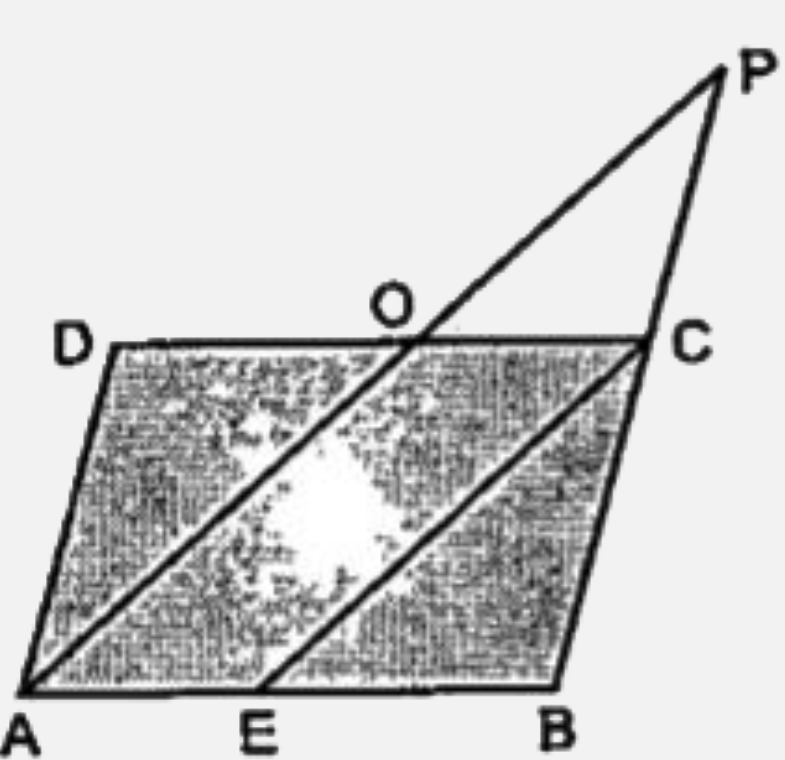
BP=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
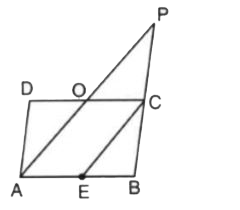
PB=2AD
View SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E. Prove that :
PQ is parallel to AB.
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:

O is mid-point of AP.
View SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP product meets CD produced at point E. Prove that :
Point P bisects BE,
View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View SolutionIn parallelogram ABCD, E is mid-point of CD and through D, a line is drawn parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that :
DG = 2EB
View SolutionIn parallelogram ABCD, E is mid-point of CD and through D, a line is drawr parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that:
2×AD=GC
View SolutionIn trapezium ABCD, AB//DC. M is mid point of AD and N is mid-point of BC.
If AB = 8 cm and DC = 11 cm , find MN.
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
View Solution
