The area enclosed between the curve y=loge(x+e) and the coordinate axes is
A
4 sq units
B
3 sq units
C
2 sq units
D
1 sq unit
Video Solution
Text Solution
The correct Answer is:D
A=∫o1−eloge(x+e)dx
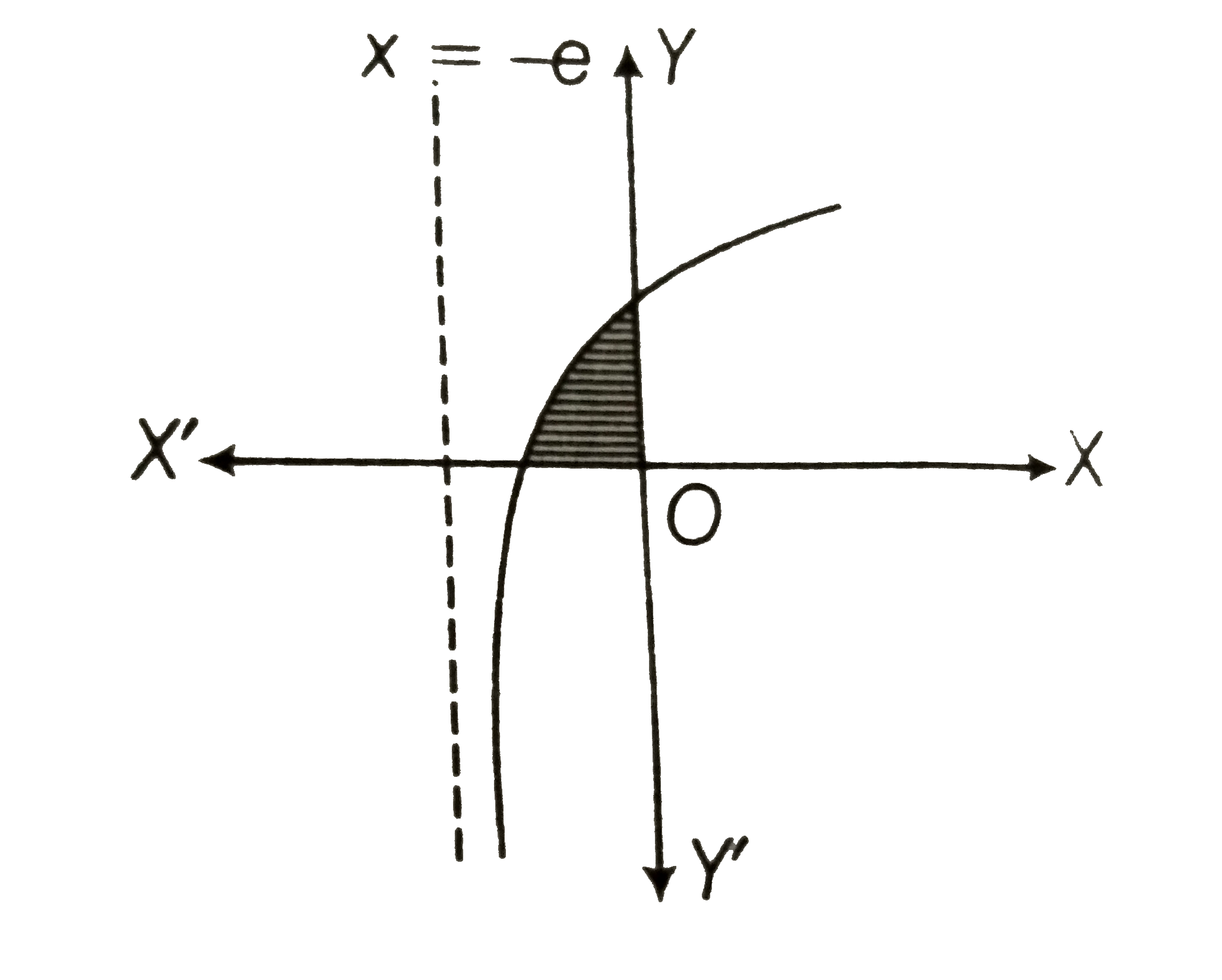
Put x+e=t⇒dx=dt
∴ A=∫e1logt dt=[tlogt−t]e1
=(e−e−0+1)=1 sq unit
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The area enclosed between the curve y=loge(x+e) and the coordinate axes is
A3B4C1D2 - Question 2 - Select One
What is the area between the curve y=cos3x,0≤x≤π6 and the coordinate axes?
A1 sq. unitB12 sq. unitC13 sq. unitD14 sq. unit - Question 3 - Select One
Area enclosed between the curve y2=x and the line y = x is
A1B13C16D15
The area enclosed by the curve y=(x−1)(x−2)(x−3) between the coordinate axes and the ordinate at x=3 is
View SolutionThe area enclosed between the curves y=∣∣x3∣∣ and x=y3 is
View SolutionFind the area enclosed between the curve y=logx1, X-axis and ordinates x=12andx=32.
View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is 2sq.units (b) 1sq.units 4sq.units (d) none of these
View SolutionThe area enclosed between the curves y=x3 and y=√x is
View Solution

