The objective function of an LPP is A) a constraint B)a function to be optimised C) a relation between the variables D) none of these
a constraint
a function to be optimised
a relation between the variables
None of the above
The correct Answer is:B
To solve the question regarding the objective function of a Linear Programming Problem (LPP), we can break it down step by step.
1. Understanding LPP:
A Linear Programming Problem (LPP) involves optimizing a linear objective function, subject to a set of linear inequalities or equations known as constraints.
Hint: Remember that LPP is used to find the best outcome in a mathematical model whose requirements are represented by linear relationships.
2. Objective Function:
The objective function in an LPP is the function that we want to maximize or minimize. It is typically expressed in the form:
Z=c1x1+c2x2+...+cnxn
where Z is the objective function, c1,c2,...,cn are the coefficients, and x1,x2,...,xn are the decision variables.
Hint: Identify the coefficients and variables in the objective function; they represent the quantities you are trying to optimize.
3. Maximization and Minimization:
Depending on the problem, the objective function can either be maximized (e.g., profit) or minimized (e.g., cost). The goal is to find the optimal values of the decision variables that yield the best value of the objective function.
Hint: Determine whether the context of the problem requires you to maximize or minimize the objective function.
4. Conclusion:
Therefore, the objective function of an LPP is the function that is to be optimized (either maximized or minimized) based on the constraints provided.
Hint: Always check the constraints as they will guide you in finding the feasible region for the optimization.
Final Answer:
The objective function of an LPP is the function that is to be optimized (maximized or minimized) based on the constraints of the problem.
A Linear Programming Problem (LPP) involves optimizing a linear objective function, subject to a set of linear inequalities or equations known as constraints.
The objective function in an LPP is the function that we want to maximize or minimize. It is typically expressed in the form:
Z=c1x1+c2x2+...+cnxn
where Z is the objective function, c1,c2,...,cn are the coefficients, and x1,x2,...,xn are the decision variables.
Depending on the problem, the objective function can either be maximized (e.g., profit) or minimized (e.g., cost). The goal is to find the optimal values of the decision variables that yield the best value of the objective function.
Therefore, the objective function of an LPP is the function that is to be optimized (either maximized or minimized) based on the constraints provided.
The objective function of an LPP is the function that is to be optimized (maximized or minimized) based on the constraints of the problem.
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )
15 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Knowledge Check
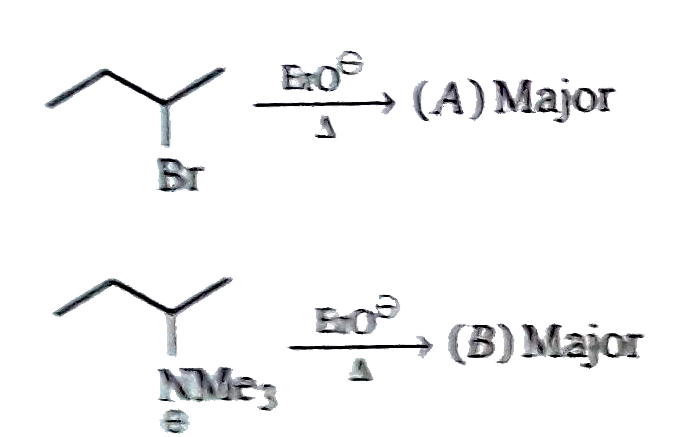
relation between (A) an d(B) is :AGgtIBPostitional isomerCEnanttiomerDChain isomerThe objective function off LPP defined over the convex set attains it optimum value at
Atleast two off the corner value atBall the corner pointsCatleast one of the corner pointsDnone of the corner points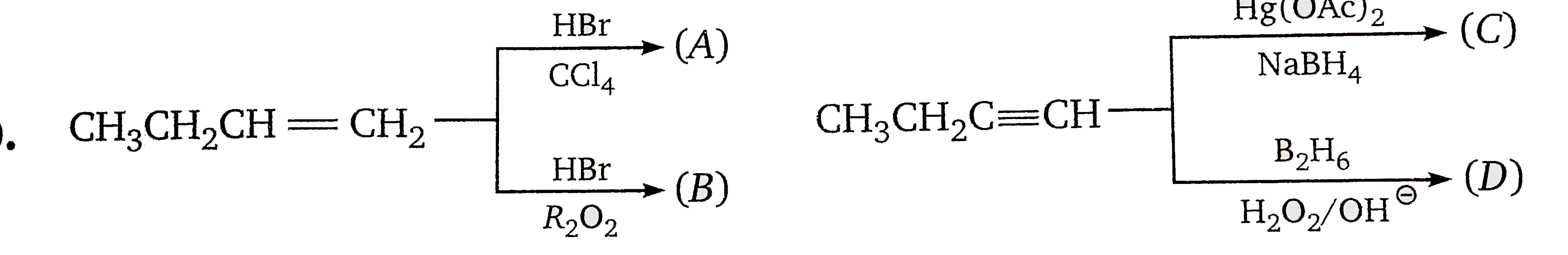
Relation between A and B, C and D are:APosition, chainBPosition, FunctionalCChain, IdenticalDMetamer, Functional
Objective function of LPP is a relation between the decision variables. (True/False)
View SolutionRelation between graphs of a function and its inverse
View SolutionThe Keynesian consumption function shows a relation between
View SolutionThe value of objective function is maximum under linear constraints
View SolutionThe value of an objective function is maximum under linear constraints:
View Solution
