Suppose ana attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2, (a) Write down the dimensional formulae and appporpriate SI units of C and k. (b) Suppose that k=1fermi−1 and that the repulsive electreic force between the protons is just blanced by the attractive nuclear force when the separation is 5 fermi. Find the value of c.
To solve the problem step by step, we will break it down into parts (a) and (b) as specified in the question.
Part (a): Dimensional Formulae and SI Units of C and k
1. Understanding the Force Equation: The attractive nuclear force between two protons is given by:
F=Ce−krr2
Here, F is the force, C is a constant, k is a constant related to the range of the force, and r is the separation between the protons.
2. SI Unit of Force: The SI unit of force F is Newton (N).
3. Finding the Unit of C:
- Rearranging the force equation gives:
C=F⋅r2⋅ekr
- Since e−kr is a dimensionless quantity, we can ignore it for dimensional analysis.
- Therefore, the unit of C is:
Unit of C=Unit of F⋅Unit of r2=N⋅m2
- Thus, the SI unit of C is N m2.
4. Finding the Unit of k:
- The term kr must be dimensionless, so:
(k)⋅(r)=1⇒(k)=1(r)
- The unit of r is meter (m), hence:
(k)=m−1
- Therefore, the SI unit of k is m−1.
5. Dimensional Formula of C:
- The dimensional formula for force F is:
(F)=(MLT−2)
- Therefore, the dimensional formula for C is:
(C)=(F)⋅(r2)=(MLT−2)⋅(L2)=(ML3T−2)
6. Dimensional Formula of k:
- Since k has the unit of m−1, its dimensional formula is:
(k)=(L−1)
Summary of Part (a):
- SI Units:
- C: N m²
- k: m⁻¹
- Dimensional Formulae:
- C: (ML3T−2)
- k: (L−1)
---
Part (b): Finding the Value of C
1. Given Information:
- k=1Fermi−1
- Separation r=5Fermi
- The electrostatic force is balanced by the nuclear force.
2. Electric Force Between Protons:
- The electric force Fe is given by Coulomb's law:
Fe=keq1q2r2
- Here, ke is Coulomb's constant (9×109N m2/C2), and q1=q2=e (the charge of a proton, 1.6×10−19C).
- Therefore, substituting the values:
Fe=(9×109)(1.6×10−19)2(5×10−15)2
3. Calculating Fe:
- Calculate (1.6×10−19)2=2.56×10−38
- Calculate (5×10−15)2=25×10−30=2.5×10−29
- Thus:
Fe=(9×109)(2.56×10−38)2.5×10−29=23.04×10−292.5×10−29=9.216N
4. Nuclear Force:
- The nuclear force at r=5Fermi:
Fn=Ce−k⋅rr2
- With k=1Fermi−1 and r=5Fermi:
Fn=Ce−5(5×10−15)2
5. Setting Forces Equal:
- Since Fe=Fn:
9.216=Ce−5(5×10−15)2
- Rearranging gives:
C=9.216⋅(5×10−15)2⋅e5
6. Calculating C:
- Calculate (5×10−15)2=25×10−30=2.5×10−29
- Thus:
C=9.216⋅2.5×10−29⋅e5
- Using e5≈148.41:
C≈9.216⋅2.5×10−29⋅148.41≈3.4×1026N m2
Summary of Part (b):
- The value of C is approximately 3.4×1026N m2.
---
F=Ce−krr2
Here, F is the force, C is a constant, k is a constant related to the range of the force, and r is the separation between the protons.
- Rearranging the force equation gives:
C=F⋅r2⋅ekr
- Since e−kr is a dimensionless quantity, we can ignore it for dimensional analysis.
- Therefore, the unit of C is:
Unit of C=Unit of F⋅Unit of r2=N⋅m2
- Thus, the SI unit of C is N m2.
- The term kr must be dimensionless, so:
(k)⋅(r)=1⇒(k)=1(r)
- The unit of r is meter (m), hence:
(k)=m−1
- Therefore, the SI unit of k is m−1.
- The dimensional formula for force F is:
(F)=(MLT−2)
- Therefore, the dimensional formula for C is:
(C)=(F)⋅(r2)=(MLT−2)⋅(L2)=(ML3T−2)
- Since k has the unit of m−1, its dimensional formula is:
(k)=(L−1)
- SI Units:
- C: N m²
- k: m⁻¹
- Dimensional Formulae:
- C: (ML3T−2)
- k: (L−1)
- k=1Fermi−1
- Separation r=5Fermi
- The electrostatic force is balanced by the nuclear force.
- The electric force Fe is given by Coulomb's law:
Fe=keq1q2r2
- Here, ke is Coulomb's constant (9×109N m2/C2), and q1=q2=e (the charge of a proton, 1.6×10−19C).
- Therefore, substituting the values:
Fe=(9×109)(1.6×10−19)2(5×10−15)2
- Calculate (1.6×10−19)2=2.56×10−38
- Calculate (5×10−15)2=25×10−30=2.5×10−29
- Thus:
Fe=(9×109)(2.56×10−38)2.5×10−29=23.04×10−292.5×10−29=9.216N
- The nuclear force at r=5Fermi:
Fn=Ce−k⋅rr2
- With k=1Fermi−1 and r=5Fermi:
Fn=Ce−5(5×10−15)2
- Since Fe=Fn:
9.216=Ce−5(5×10−15)2
- Rearranging gives:
C=9.216⋅(5×10−15)2⋅e5
- Calculate (5×10−15)2=25×10−30=2.5×10−29
- Thus:
C=9.216⋅2.5×10−29⋅e5
- Using e5≈148.41:
C≈9.216⋅2.5×10−29⋅148.41≈3.4×1026N m2
- The value of C is approximately 3.4×1026N m2.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
8 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
The gravitational force between two point masses m1 and m2 at separation r is given by F=km1m2r2
The constant k doesn't
View SolutionThe amount of charge passed in time t through a cross-section of a wire is
Q(t)=At2+Bt+C.
(a)Write the dimensional formulae for A,B and C.
(b) If the numerical values of A,B,and C are 5,3 and 1 respectively in SI units,find the value of the current at t=5 s.
View Solution
Knowledge Check
Find the electric force between two protons separated by a distance of 1 fermi (1fermi=1015m). The protons in a nucleus remain at a separation of this order.
A230NB2300NC23000NDNone of the AboveWhen air is replaced by a dielectric medium of dielectric constant K, the force at attraction between two charges q1andq2 separated by a finite distance 'd'
Adecreases K timesBincreases K timesCremains unchargedDdecreases K2 times.The gravitional force between two point masses m1 and m2 at separation r is given by F=km1m2r2
The constant kADepends on system of units onlyBDepends on medium between masses onlyCDepends on both (a) and (b)DIs independent of both (a) and (b)
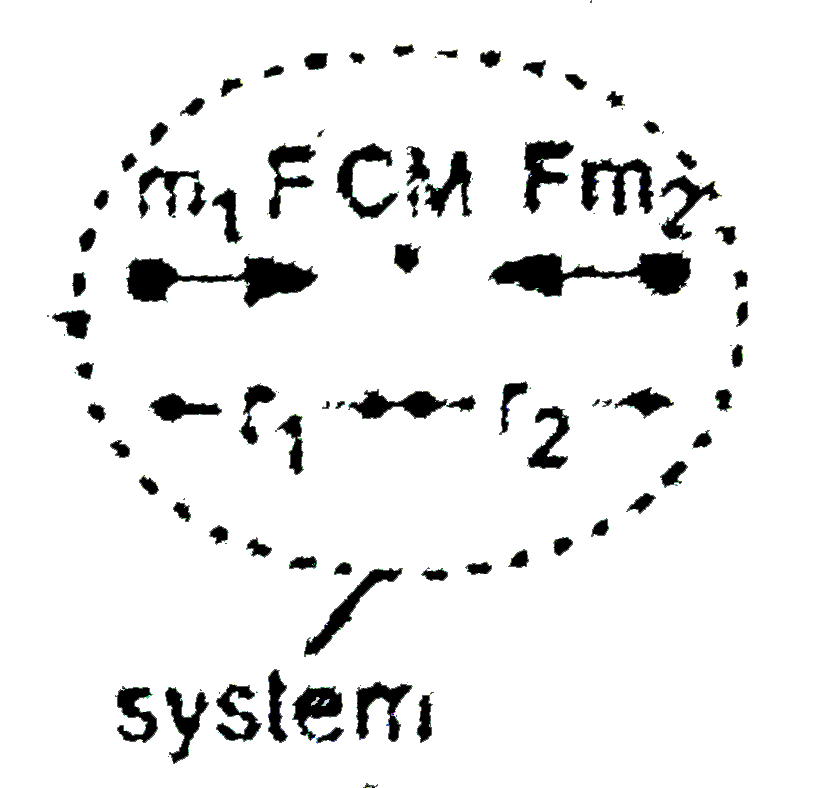
Consider a system of two particles of masses m1 and m2 separated by a distance r. Suppose they start to move towards each other due to their mutual attraction (attractive force may be electrical, gravitational, etc.).
View SolutionCoulomb's law for electrostatic force between two point charges and Newton's law for gravitational force between two stationary point masses, both have inverse square dependence on the distance between the charges/masses (a) compare the strength of these forces by determining the ratio of their magnitudes (i) for an electron and as proton (ii) for two protons (b) estimate the accelerations for election and proton due to electrical force of their mutal attraction when they are 1 A apart.
View Solution(a) Two protons are placed at some separation in vacuum. Find the ratio of electric and gravitational force acting between them.
(b) Two point charges are placed at separation 3m in vacuum. What can be the minimum force between them.
(c ) A charge Q is to be divided on two objects. What should be the value of the charges in the objects so that the force between them is maximum ?
(d) Two insulating small spheres are rubbed against each other and placed 1.6cm apart. If they attract each other with a force of 0.9N, how many electrons were transferred from one sphere to the other during rubbing ?
View SolutionTwo nucleons are at a separation of 1 fermi. The net force between them is F1, if both are neutrons F2, if both are protons and F3, if one is a proton and the other is a neutron
View SolutionThe electrostatic force between two point charges q1 and q2 at separation r is given by F=k.q1q2r2. The constant k
View Solution
