Three equal charges, 2.0×10−6 C each, are held fixed at the three corners of a square of side 5 cm. find the Coulomb force experienced by one of the charges due to the rest two.
To solve the problem of finding the Coulomb force experienced by one of the charges due to the other two charges, we can follow these steps:
1. Identify the Charges and Configuration:
- We have three equal charges, each of magnitude q=2.0×10−6C.
- These charges are placed at the corners of a square with side length a=5cm=0.05m.
2. Calculate the Force Between Two Charges:
- The force between any two charges can be calculated using Coulomb's Law:
F=kq1q2r2
- Here, k is Coulomb's constant, k≈9×109N m2/C2.
- Since all charges are equal, we can denote them as q and the distance r between any two charges is equal to the side of the square, r=0.05m.
3. Calculate the Force F Between Two Charges:
- Substituting the values into Coulomb's Law:
F=kq2r2=9×109(2.0×10−6)2(0.05)2
- Calculate F:
F=9×1094.0×10−120.0025=9×109×1.6×10−9=14.4N
4. Determine the Net Force on One Charge:
- The net force on one charge due to the other two charges needs to be calculated.
- Since the charges are at the corners of a square, the angle between the forces due to the two other charges is 90∘.
- The resultant force can be found using vector addition. If F is the force due to each of the other charges, the net force Fnet can be calculated as:
Fnet=√F2+F2=√2F2=F√2
- However, we must consider the angle between the forces. The angle between the forces is 45∘ because of symmetry.
5. Calculate the Components of the Forces:
- The components of the forces can be calculated as:
Fnet=2Fcos(45∘)=2F1√2=F√2
- Substitute F=14.4N:
Fnet=14.4√2≈20.4N
Final Result
The total Coulomb force experienced by one of the charges due to the other two charges is approximately 20.4 N.
- We have three equal charges, each of magnitude q=2.0×10−6C.
- These charges are placed at the corners of a square with side length a=5cm=0.05m.
- The force between any two charges can be calculated using Coulomb's Law:
F=kq1q2r2
- Here, k is Coulomb's constant, k≈9×109N m2/C2.
- Since all charges are equal, we can denote them as q and the distance r between any two charges is equal to the side of the square, r=0.05m.
- Substituting the values into Coulomb's Law:
F=kq2r2=9×109(2.0×10−6)2(0.05)2
- Calculate F:
F=9×1094.0×10−120.0025=9×109×1.6×10−9=14.4N
- The net force on one charge due to the other two charges needs to be calculated.
- Since the charges are at the corners of a square, the angle between the forces due to the two other charges is 90∘.
- The resultant force can be found using vector addition. If F is the force due to each of the other charges, the net force Fnet can be calculated as:
Fnet=√F2+F2=√2F2=F√2
- However, we must consider the angle between the forces. The angle between the forces is 45∘ because of symmetry.
- The components of the forces can be calculated as:
Fnet=2Fcos(45∘)=2F1√2=F√2
- Substitute F=14.4N:
Fnet=14.4√2≈20.4N
The total Coulomb force experienced by one of the charges due to the other two charges is approximately 20.4 N.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
8 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
Four equal charges 2.0×10−6C each are fixed at the four corners of a squae of side 5 cm. Find the coulomba force eperienced by one of the charges due to the rest three.
View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View Solution
Knowledge Check
Equal charges q are placed at the three corners B, C, D of a square ABCD of side a. The potential at A is
A14πε0qaB3q4πε0Cq4πε0a[2+1√2]Dq4πε0a[1+√2]Charges of +103×10−9C are placed at each of the four corners of a square of side 8cm. The potential at the intersection of the diagonals is
A150√2 voltB1500√2 voltC900√2 voltD900 volt
Three equal charges, each having a magnitude of 2×10−6C, are placed at the three corners of a right-angled triangle of sides 3, 4, and 5 cm. Find the force on the charge at the right-angled corner.
View Solution(i) Three equak charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out dorce acting on one of the charge due to other two charges ?
(ii) In the above question, if one of the charge is replaced by negative charge then find out force acting on it due to other charges ?
(iii) Repeat the part (i) if magnitude of each charge is doubled and side of triangle is reduced to half.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree identical charges of q each are placed at the three verticess of an equilateral triangle ABC of side a, Electrostatic force experienced by a point charge q0 situated at the centroid G of triangle is ___________
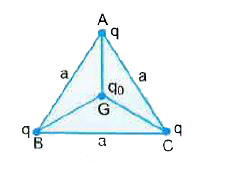
View SolutionThree equal charges, each having a magnitude of. 2.0×10−6C, are placed at the thre corners of a right. angled triangle of sides 3 cm, 4cm and 5 cm. find the three corner.
View SolutionEight equal charged are placed at the eight corners of a cubewhich is a on each side . Calculate the force experienced by each charge q.
View Solution
